We have learnt about various aspects of motion along a straight line: kinematics (where we learned about displacement, velocity, and acceleration), projectile motion (a special case of two-dimensional kinematics), force, and Newton’s laws of motion. Newton’s first law tells us that objects move along a straight line at constant speed unless a net external force acts on them. Therefore, if an object moves along a circular path, it must be experiencing an external force. In this chapter, we explore both circular motion and rotational motion.

Angle of Rotation and Angular Velocity

What exactly do we mean by circular motion or rotation? Rotational motion is the circular motion of an object about an axis of rotation. We will discuss specifically circular motion and spin. Circular motion is when an object moves in a circular path.

Examples of circular motion include a race car speeding around a circular curve, a toy attached to a string swinging in a circle around your head. Spin is rotation about an axis that goes through the center of mass of the object, such as Earth rotating on its axis, a wheel turning on its axle, the spin of a tornado on its path of destruction, or a figure skater spinning during a performance at the Olympics. Sometimes, objects will be spinning while in circular motion, like the Earth spinning on its axis while revolving around the Sun, but we will focus on these two motions separately.

When solving problems involving rotational motion, we use variables that are similar to linear variables (distance, velocity, acceleration, and force) but take into account the curvature or rotation of the motion. Here, we define the angle of rotation, which is the angular equivalence of distance; and angular velocity, which is the angular equivalence of linear velocity.

When objects rotate about some axis—for example, when the CD in the below figure rotates about its center—each point in the object follows a circular path.

All points on a CD travel in circular paths. The pits (dots) along a line from the center to the edge all move through the same angle Δθ in time Δt

The arc length, , is the distance travelled along a circular path. The radius of curvature, r, is the radius of the circular path. Both are shown in the below figure

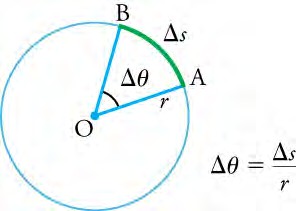
The radius (r) of a circle is rotated through an angle Δθ . The arc length, ΔS, is the distance covered along the circumference.

Consider a line from the center of the CD to its edge. In a given time, each pit (used to record information) on this line moves through the same angle. The angle of rotation is the amount of rotation and is the angular analog of distance. The angle of rotation Δθ is the arc length divided by the radius of curvature

Δθ = ΔS / r

The angle of rotation is often measured by using a unit called the radian. (Radians are actually dimensionless, because a radian is defined as the ratio of two distances, radius and arc length.) A revolution is one complete rotation, where every point on the circle returns to its original position. One revolution covers 2π radians (or 360 degrees), and therefore has an angle of rotation of 2π radians, and an arc length that is the same as the circumference of the circle. We can convert between radians, revolutions, and degrees using the relationship

1 revolution = 2π rad = 360°. See the below for the conversion of degrees to radians for some common angles

2 π rad = 360⁰

1 rad = 360⁰ / 2 π

1 rad ≈ 57.3 ⁰

Degree Measures	Radian Measure
300	π/ 6
600	π/ 3
900	π/ 2
1200	2π/ 3
1350	3π/ 4
1800	π

Angular Velocity

How fast is an object rotating? We can answer this question by using the concept of angular velocity. Consider first the angular speed ω is the rate at which the angle of rotation changes. In equation form, the angular speed is

ω = Δθ / Δ t

which means that an angular rotation Δθ occurs in a time, Δt. If an object rotates through a greater angle of rotation in a given time, it has a greater angular speed. The units for angular speed are radians per second (rad/s).

Now let’s consider the direction of the angular speed, which means we now must call it the angular velocity. The direction of the angular velocity is along the axis of rotation. For an object rotating clockwise, the angular velocity points away from you along the axis of rotation. For an object rotating counterclockwise, the angular velocity points toward you along the axis of rotation.

Angular velocity (ω) is the angular version of linear velocity v. Tangential velocity is the instantaneous linear velocity of an object in rotational motion. To get the precise relationship between angular velocity and tangential velocity, consider again a pit on the rotating CD. This pit moves through an arc length  Δs  in a short time  Δt so its tangential speed is

V = Δs / Δt

From the definition of the angle of rotation, we know that

Δϑ = Δs / r,

Hence , Δs = r Δϑ

Substituting this into the expression for v gives

V = r Δϑ / Δt

V = r ω

The equation V = r ω says that the tangential speed v is proportional to the distance r from the center of rotation. Consequently, tangential speed is greater for a point on the outer edge of the CD (with larger r) than for a point closer to the center of the CD (with smaller r). This makes sense because a point farther out from the center has to cover a longer arc length in the same amount of time as a point closer to the center. Note that both points will still have the same angular speed, regardless of their distance from the center of rotation

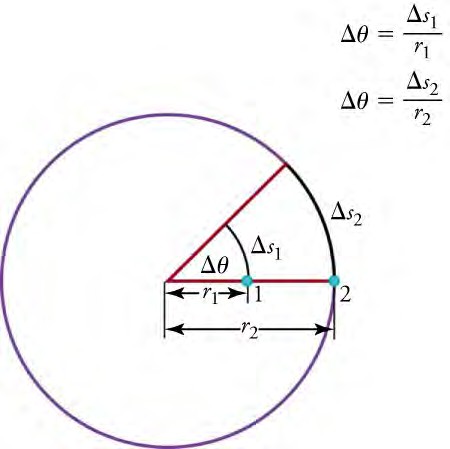
Points 1 and 2 rotate through the same angle (Δθ), but point 2 moves through a greater arc length (Δs₂) because it is farther from the center of rotation.

Now, consider another example: the tire of a moving car . The faster the tire spins, the faster the car moves—large  means large v because . Similarly, a larger-radius tire rotating at the same angular velocity, , will produce a greater linear (tangential) velocity, v, for the car. This is because a larger radius means a longer arc length must contact the road, so the car must move farther in the same amount of time

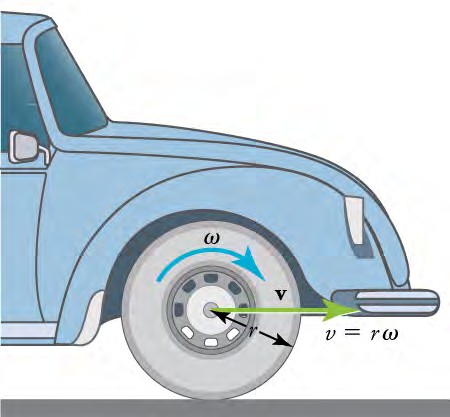
A car moving at a velocity, v, to the right has a tire rotating with angular velocity ω . The speed of the tread of the tire relative to the axle is v, the same as if the car were jacked up and the wheels spinning without touching the road. Directly below the axle, where the tire touches the road, the tire tread moves backward with respect to the axle with tangential velocity v=rω, where r is the tire radius.

Because the road is stationary with respect to this point of the tire, the car must move forward at the linear velocity v. A larger angular velocity for the tire means a greater linear velocity for the car.

However, there are cases where linear velocity and tangential velocity are not equivalent, such as a car spinning its tires on ice. In this case, the linear velocity will be less than the tangential velocity. Due to the lack of friction under the tires of a car on ice, the arc length through which the tire treads move is greater than the linear distance through which the car moves. It’s similar to running on a treadmill or pedaling a stationary bike; you are literally going nowhere fast

Uniform Circular Motion

In the previous section, we defined circular motion. The simplest case of circular motion is uniform circular motion, where an object travels a circular path at a constant speed. Note that, unlike speed, the linear velocity of an object in circular motion is constantly changing because it is always changing direction. We know from kinematics that acceleration is a change in velocity, either in magnitude or in direction or both. Therefore, an object undergoing uniform circular motion is always accelerating, even though the magnitude of its velocity is constant.

You experience this acceleration yourself every time you ride in a car while it turns a corner. If you hold the steering wheel steady during the turn and move at a constant speed, you are executing uniform circular motion. What you notice is a feeling of sliding (or being flung, depending on the speed) away from the center of the turn. This isn’t an actual force that is acting on you—it only happens because your body wants to continue moving in a straight line (as per Newton’s first law) whereas the car is turning off this straight-line path. Inside the car it appears as if you are forced away from the center of the turn. This fictitious force is known as the centrifugal force. The sharper the curve and the greater your speed, the more noticeable this effect becomes.

Below figure shows an object moving in a circular path at constant speed. The direction of the instantaneous tangential velocity is shown at two points along the path. Acceleration is in the direction of the change in velocity; in this case it points roughly toward the center of rotation. (The center of rotation is at the center of the circular path). If we imagine  becoming smaller and smaller, then the acceleration would point exactly toward the center of rotation, but this case is hard to draw. We call the acceleration of an object moving in uniform circular motion the centripetal acceleration a_c because centripetal means center seeking.

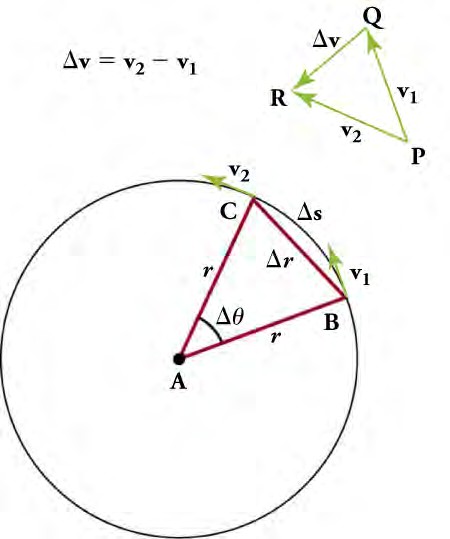
The directions of the velocity of an object at two different points are shown, and the change in velocity  is seen to point approximately toward the center of curvature (see small inset). For an extremely small value of Δs, Δv points exactly toward the center of the circle (but this is hard to draw). Because ac = Δv/Δt, the acceleration is also toward the center, so a_c is called centripetal acceleration.

Now that we know that the direction of centripetal acceleration is toward the center of rotation, let’s discuss the magnitude of centripetal acceleration. For an object traveling at speed v in a circular path with radius r, the magnitude of centripetal acceleration is

a_c  = v² / r

Centripetal acceleration is greater at high speeds and in sharp curves (smaller radius), as you may have noticed when driving a car, because the car actually pushes you toward the center of the turn. But it is a bit surprising that a_c is proportional to the speed squared. This means, for example, that the acceleration is four times greater when you take a curve at 100 km/h than at 50 km/h

We can also express a_c in terms of the magnitude of angular velocity. Substituting v = rω into the equation above, we get

a_c = (rω)² / r = rω²

Centripetal Force

Because an object in uniform circular motion undergoes constant acceleration (by changing direction), we know from Newton’s second law of motion that there must be a constant net external force acting on the object.

Any force or combination of forces can cause a centripetal acceleration. Just a few examples are the tension in the rope on a tether ball, the force of Earth’s gravity on the Moon, the friction between a road and the tires of a car as it goes around a curve, or the normal force of a roller coaster track on the cart during a loop-the-loop.

Any net force causing uniform circular motion is called a centripetal force. The direction of a centripetal force is toward the center of rotation, the same as for centripetal acceleration. According to Newton’s second law of motion, a net force causes the acceleration of mass according to F_net = ma. For uniform circular motion, the acceleration is centripetal acceleration: a = a_c.

Therefore, the magnitude of centripetal force, F_c, is F_c = ma_c

By using the two different forms of the equation for the magnitude of centripetal acceleration, a_c=v²/r and a_c = rω², we get two expressions involving the magnitude of the centripetal force F_c. The first expression is in terms of tangential speed, the second is in terms of angular speed:
F_c = m v²/r and F_c = mω².

Both forms of the equation depend on mass, velocity, and the radius of the circular path. You may use whichever expression for centripetal force is more convenient. Newton’s second law also states that the object will accelerate in the same direction as the net force. By definition, the centripetal force is directed towards the center of rotation, so the object will also accelerate towards the center. A straight line drawn from the circular path to the center of the circle will always be perpendicular to the tangential velocity. Note that, if you solve the first expression for r, you get

r = mv² / F_c

From this expression, we see that, for a given mass and velocity, a large centripetal force causes a small radius of curvature—that is, a tight curve

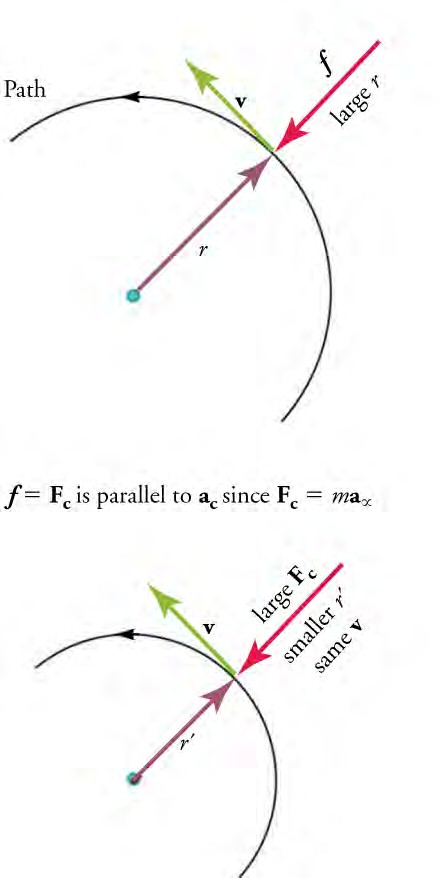
In this figure, the frictional force f serves as the centripetal force F_c. Centripetal force is perpendicular to tangential velocity and causes uniform circular motion. The larger the centripetal force F_c, the smaller is the radius of curvature r and the sharper is the curve. The lower curve has the same velocity v, but a larger centripetal force F_c produces a smaller radius r‘.

Rotational Motion

In the section on uniform circular motion, we discussed motion in a circle at constant speed and, therefore, constant angular velocity. However, there are times when angular velocity is not constant—rotational motion can speed up, slow down, or reverse directions. Angular velocity is not constant when a spinning skater pulls in her arms, when a child pushes a merry-go-round to make it rotate, or when a CD slows to a halt when switched off. In all these cases, angular acceleration occurs because the angular velocity ω changes. The faster the change occurs, the greater is the angular acceleration. Angular acceleration α is the rate of change of angular velocity. In equation form, angular acceleration is

α = Δω / Δt

where Δω is the change in angular velocity and Δt is the change in time. The units of angular acceleration are (rad/s)/s, or rad/s². If ω increases, then α is positive. If ω decreases, then α is negative. Keep in mind that, by convention, counterclockwise is the positive direction and clockwise is the negative direction. For example, a skater rotates counterclockwise as seen from above, so her angular velocity is positive. Acceleration would be negative, for example, when an object that is rotating counterclockwise slows down. It would be positive when an object that is rotating counterclockwise speeds up.

The relationship between the magnitudes of tangential acceleration, a, and angular acceleration,
α, isa = rαorα = a/r.

These equations mean that the magnitudes of tangential acceleration and angular acceleration are directly proportional to each other. The greater the angular acceleration, the larger the change in tangential acceleration, and vice versa.

Rotational  Linear Relationship

θ	x	θ = x/r
ω	v	ω = v/r
α	a	α = a/r

We can now begin to see how rotational quantities like θ, ω and α are related to each other. For example, if a motorcycle wheel that starts at rest has a large angular acceleration for a fairly long time, it ends up spinning rapidly and rotates through many revolutions. Putting this in terms of the variables, if the wheel’s angular acceleration α is large for a long period of time t, then the final angular velocity ω and angle of rotation θ are large. In the case of linear motion, if an object starts at rest and undergoes a large linear acceleration, then it has a large final velocity and will have traveled a large distance.

The kinematics of rotational motion describes the relationships between the angle of rotation, angular velocity, angular acceleration, and time. It only describes motion—it does not include any forces or masses that may affect rotation (these are part of dynamics). Recall the kinematics equation for linear motion:    v = v₀ + at (constant a)

As in linear kinematics, we assume a is constant, which means that angular acceleration α is also a constant, because
a = r α

The equation for the kinematics relationship between ω, α, and t is
ω = ω₀ + αt (constant α),

where ω₀ is the initial angular velocity. Notice that the equation is identical to the linear version, except with angular analogs of the linear variables. In fact, all of the linear kinematics equations have rotational analogs, which are given in Table 6.3. These equations can be used to solve rotational or linear kinematics problem in which a and αare constant.

Torque

If you have ever spun a bike wheel or pushed a merry-go-round, you know that force is needed to change angular velocity. The farther the force is applied from the pivot point (or fulcrum), the greater the angular acceleration. For example, a door opens slowly if you push too close to its hinge, but opens easily if you push far from the hinges. Furthermore, we know that the more massive the door is, the more slowly it opens; this is because angular acceleration is inversely proportional to mass. These relationships are very similar to the relationships between force, mass, and acceleration from Newton’s second law of motion. Since we have already covered the angular versions of distance, velocity and time, you may wonder what the angular version of force is, and how it relates to linear force.

The angular version of force is torque , which is the turning effectiveness of a force. See the below figure. The equation for the magnitude of torque is

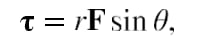
where r is the magnitude of the lever arm, F is the magnitude of the linear force, and θ is the angle between the lever arm and the force. The lever arm is the vector from the point of rotation (pivot point or fulcrum) to the location where force is applied. Since the magnitude of the lever arm is a distance, its units are in meters, and torque has units of N⋅m. Torque is a vector quantity and has the same direction as the angular acceleration that it produces.

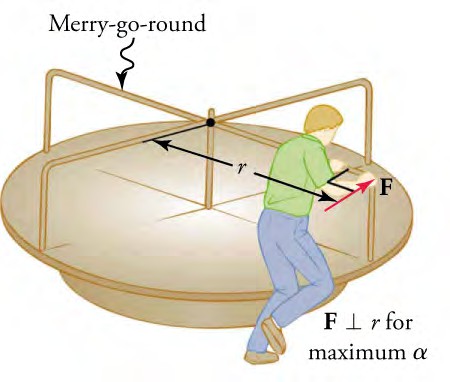
The harder the man pushes the merry-go- round in the above figure , the faster it accelerates. Furthermore, the more massive the merry-go-round is, the slower it accelerates for the same torque. If the man wants to maximize the effect of his force on the merry-go-round, he should push as far from the center as possible to get the largest lever arm and, therefore, the greatest torque and angular acceleration. Torque is also maximized when the force is applied perpendicular to the lever arm.

Just as linear forces can balance to produce zero net force and no linear acceleration, the same is true of rotational motion. When two torques of equal magnitude act in opposing directions, there is no net torque and no angular acceleration, as you can see in the following video. If zero net torque acts on a system spinning at a constant angular velocity, the system will continue to spin at the same angular velocity

Take Quiz