PROPERTIES OF SOLIDS AND LIQUIDS – 3
Table of Contents
Cohesion and Adhesion in Liquids: Surface Tension and Capillary Action
Children blow soap bubbles and play in the spray of a sprinkler on a hot summer day. (See Figure below ) . A technician draws blood into a small-diameter tube just by touching it to a drop on a pricked finger. A premature infant struggles to inflate her lungs. What is the common thread? All these activities are dominated by the attractive forces between atoms and molecules in liquids—both within a liquid and between the liquid and its surroundings.
Attractive forces between molecules of the same type are called cohesive forces. Liquids can, for example, be held in open containers because cohesive forces hold the molecules together. Attractive forces between molecules of different types are called adhesive forces. Such forces cause liquid drops to cling to window panes, for example. Lets examine effects directly attributable to cohesive and adhesive forces in liquids.
Cohesive Forces
Attractive forces between molecules of the same type are called cohesive forces.
Adhesive Forces
Attractive forces between molecules of different types are called adhesive forces.

The soap bubbles in this photograph are caused by cohesive forces among molecules in liquids. (credit: Steve Ford Elliott)
Surface Tension
Cohesive forces between molecules cause the surface of a liquid to contract to the smallest possible surface area. This general effect is called surface tension. Molecules on the surface are pulled inward by cohesive forces, reducing the surface area. Molecules inside the liquid experience zero net force, since they have neighbors on all sides.
Surface Tension
Cohesive forces between molecules cause the surface of a liquid to contract to the smallest possible surface area. This general effect is called surface tension.
The model of a liquid surface acting like a stretched elastic sheet can effectively explain surface tension effects. For example, some insects can walk on water (as opposed to floating in it) as we would walk on a trampoline—they dent the surface as shown in the below figure (a). The next figure (b) shows another example, where a needle rests on a water surface. The iron needle cannot, and does not, float, because its density is greater than that of water. Rather, its weight is supported by forces in the stretched surface that try to make the surface smaller or flatter. If the needle were placed point down on the surface, its weight acting on a smaller area would break the surface, and it would sink.
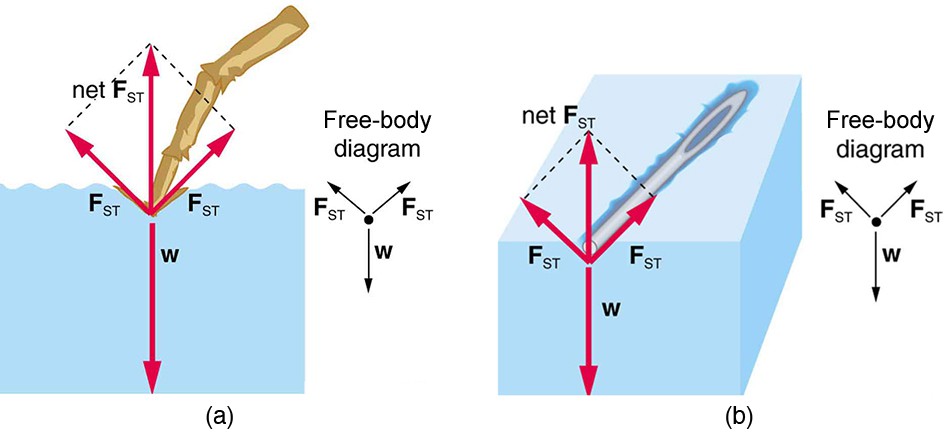
Surface tension supporting the weight of an insect and an iron needle, both of which rest on the surface without penetrating it. They are not floating; rather, they are supported by the surface of the liquid. (a) An insect leg dents the water surface. is a restoring force (surface tension) parallel to the surface. (b) An iron needle similarly dents a water surface until the restoring force (surface tension) grows to equal its weight.
Surface tension is proportional to the strength of the cohesive force, which varies with the type of liquid. Surface tension is defined to be the force F per unit length
exerted by a stretched liquid membrane
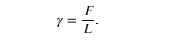
The tables below lists values of for some liquids.


For the insect of the above figure (a), its weight w is supported by the upward components of the surface tension force: w=γLsinθ, where L is the circumference of the insect’s foot in contact with the water. The figure below shows one way to measure surface tension. The liquid film exerts a force on the movable wire in an attempt to reduce its surface area. The magnitude of this force depends on the surface tension of the liquid and can be measured accurately.
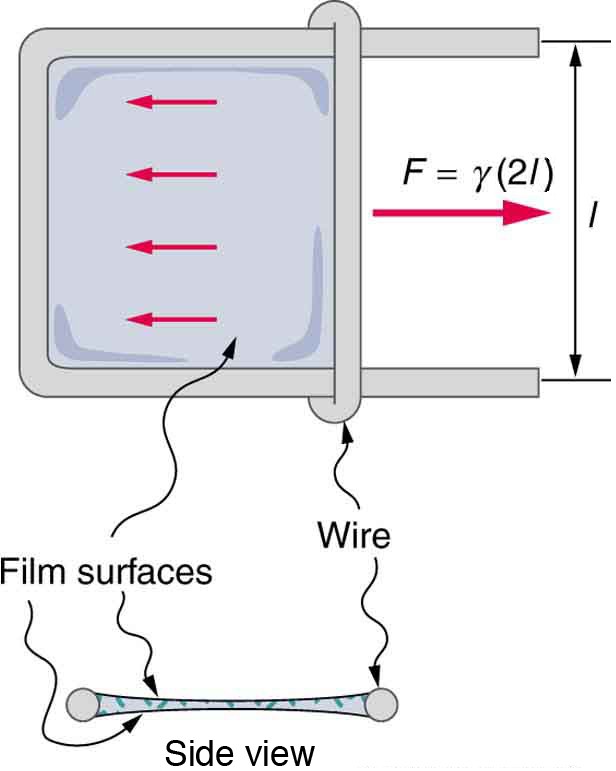
Sliding wire device used for measuring surface tension; the device exerts a force to reduce the film’s surface area. The force needed to hold the wire in place is F=γL=γ(2l), since there are two liquid surfaces attached to the wire. This force remains nearly constant as the film is stretched, until the film approaches its breaking point
Surface tension is the reason why liquids form bubbles and droplets. The inward surface tension force causes bubbles to be approximately spherical and raises the pressure of the gas trapped inside relative to atmospheric pressure outside. It can be shown that the gauge pressure P inside a spherical bubble is given by

where r is the radius of the bubble. Thus the pressure inside a bubble is greatest when the bubble is the smallest. Another bit of evidence for this is illustrated in the figure below . When air is allowed to flow between two balloons of unequal size, the smaller balloon tends to collapse, filling the larger balloon

With the valve closed, two balloons of different sizes are attached to each end of a tube. Upon opening the valve, the smaller balloon decreases in size with the air moving to fill the larger balloon. The pressure in a spherical balloon is inversely proportional to its radius, so that the smaller balloon has a greater internal pressure than the larger balloon, resulting in this flow
Our lungs contain hundreds of millions of mucus-lined sacs called alveoli, which are very similar in size, and about 0.1 mm in diameter. (See figure below.) You can exhale without muscle action by allowing surface tension to contract these sacs. Medical patients whose breathing is aided by a positive pressure respirator have air blown into the lungs, but are generally allowed to exhale on their own. Even if there is paralysis, surface tension in the alveoli will expel air from the lungs. Since pressure increases as the radii of the alveoli decrease, an occasional deep cleansing breath is needed to fully reinflate the alveoli. Respirators are programmed to do this and we find it natural
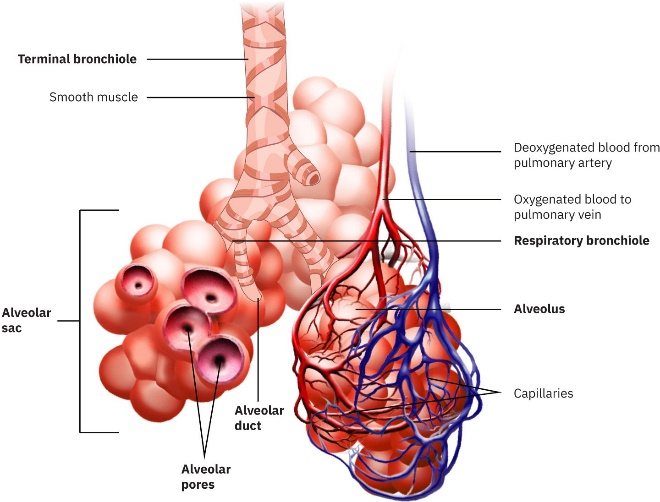
Bronchial tubes in the lungs branch into ever-smaller structures, finally ending in alveoli. The alveoli act like tiny bubbles. The surface tension of their mucous lining aids in exhalation and can prevent inhalation if too great
The tension in the walls of the alveoli results from the membrane tissue and a liquid on the walls of the alveoli containing a long lipoprotein that acts as a surfactant (a surface-tension reducing substance). The need for the surfactant results from the tendency of small alveoli to collapse and the air to fill into the larger alveoli making them even larger . During inhalation, the lipoprotein molecules are pulled apart and the wall tension increases as the radius increases (increased surface tension). During exhalation, the molecules slide back together and the surface tension decreases, helping to prevent a collapse of the alveoli. The surfactant therefore serves to change the wall tension so that small alveoli don’t collapse and large alveoli are prevented from expanding too much. This tension change is a unique property of these surfactants, and is not shared by detergents (which simply lower surface tension). (See figure below)
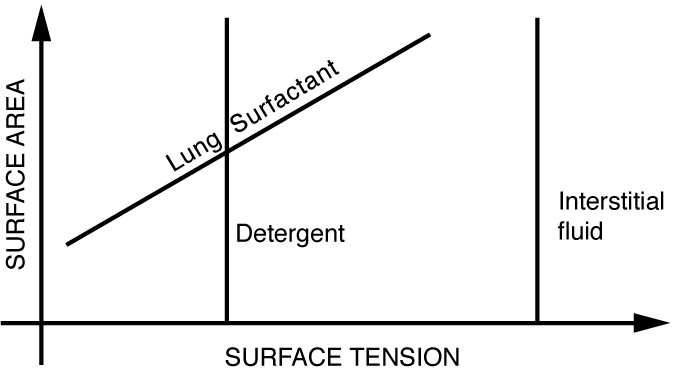
Surface tension as a function of surface area. The surface tension for lung surfactant decreases with decreasing area. This ensures that small alveoli don’t collapse and large alveoli are not able to over expand
If water gets into the lungs, the surface tension is too great and you cannot inhale. This is a severe problem in resuscitating drowning victims. A similar problem occurs in newborn infants who are born without this surfactant—their lungs are very difficult to inflate. This condition is known as hyaline membrane disease and is a leading cause of death for infants, particularly in premature births. Some success has been achieved in treating hyaline membrane disease by spraying a surfactant into the infant’s breathing passages. Emphysema produces the opposite problem with alveoli. Alveolar walls of emphysema victims deteriorate, and the sacs combine to form larger sacs. Because pressure produced by surface tension decreases with increasing radius, these larger sacs produce smaller pressure, reducing the ability of emphysema victims to exhale. A common test for emphysema is to measure the pressure and volume of air that can be exhaled.
Adhesion and Capillary Action
Why is it that water beads up on a waxed car but does not on bare paint? The answer is that the adhesive forces between water and wax are much smaller than those between water and paint. Competition between the forces of adhesion and cohesion are important in the macroscopic behavior of liquids. An important factor in studying the roles of these two forces is the angle θ between the tangent to the liquid surface and the surface. (See the figure below .) The contact angle θ is directly related to the relative strength of the cohesive and adhesive forces. The larger the strength of the cohesive force relative to the adhesive force, the larger θ is, and the more the liquid tends to form a droplet. The smaller θ is, the smaller the relative strength, so that the adhesive force is able to flatten the drop
Contact Angle
The angle θ between the tangent to the liquid surface and the surface is called the contact angle.
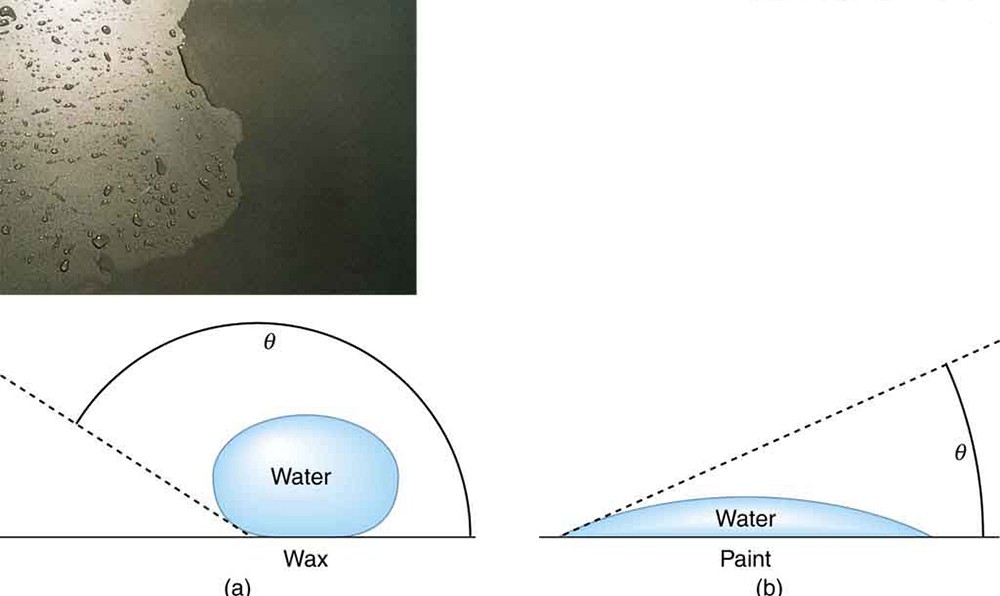
In the photograph, water beads on the waxed car paint and flattens on the unwaxed paint. (a) Water forms beads on the waxed surface because the cohesive forces responsible for surface tension are larger than the adhesive forces, which tend to flatten the drop. (b) Water beads on bare paint are flattened considerably because the adhesive forces between water and paint are strong, overcoming surface tension. The contact angle θ is directly related to the relative strengths of the cohesive and adhesive forces. The larger θ is, the larger the ratio of cohesive to adhesive forces. (credit: P. P. Urone)
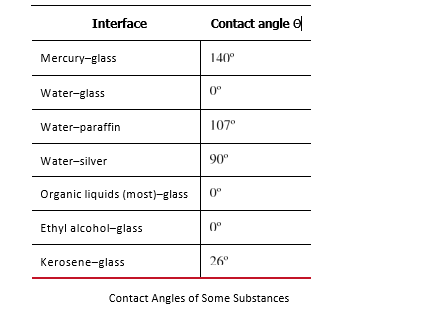
. The table below lists contact angles for several combinations of liquids and solids.
One important phenomenon related to the relative strength of cohesive and adhesive forces is capillary action—the tendency of a fluid to be raised or suppressed in a narrow tube, or capillary tube. This action causes blood to be drawn into a small-diameter tube when the tube touches a drop.
Capillary Action
The tendency of a fluid to be raised or suppressed in a narrow tube, or capillary tube, is called capillary action.
If a capillary tube is placed vertically into a liquid, as shown in the figure below , capillary action will raise or suppress the liquid inside the tube depending on the combination of substances. The actual effect depends on the relative strength of the cohesive and adhesive forces and, thus, the contact angle θ given in the table. If θ is less than 900, then the fluid will be raised; if θ is greater than 900, it will be suppressed. Mercury, for example, has a very large surface tension and a large contact angle with glass. When placed in a tube, the surface of a column of mercury curves downward, somewhat like a drop. The curved surface of a fluid in a tube is called a meniscus. The tendency of surface tension is always to reduce the surface area. Surface tension thus flattens the curved liquid surface in a capillary tube. This results in a downward force in mercury and an upward force in water, as seen in the figure below .
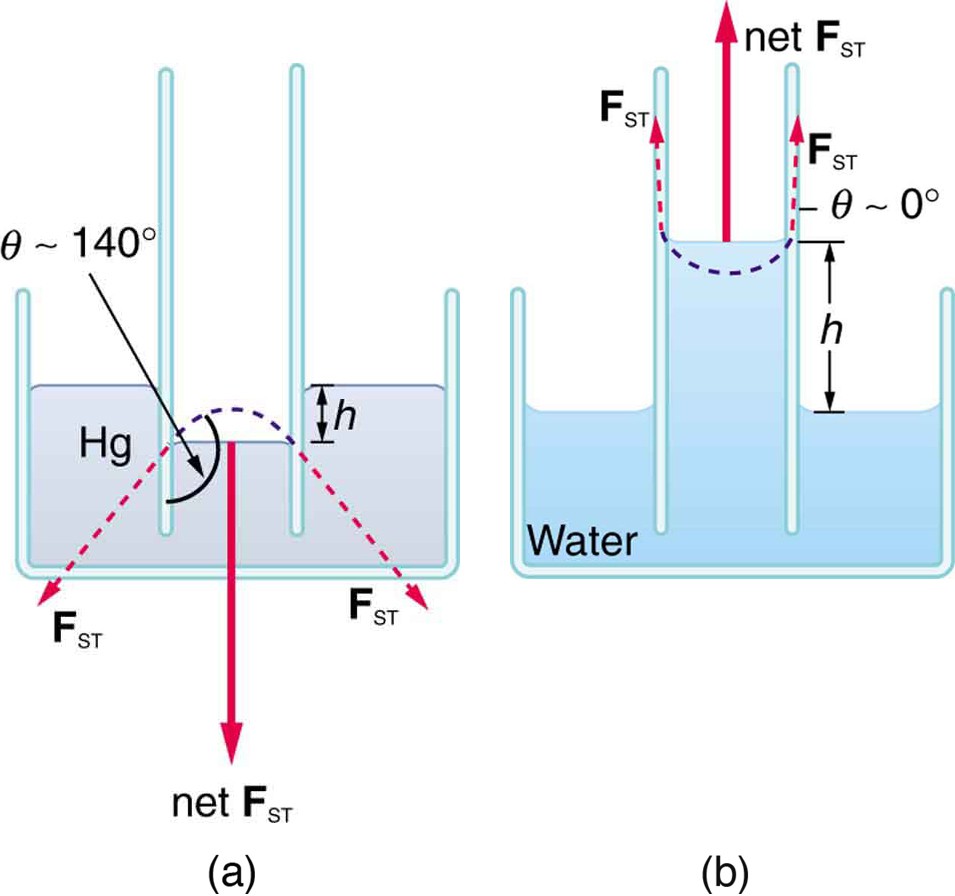
(a) Mercury is suppressed in a glass tube because its contact angle is greater than . Surface tension exerts a downward force as it flattens the mercury, suppressing it in the tube. The dashed line shows the shape the mercury surface would have without the flattening effect of surface tension. (b) Water is raised in a glass tube because its contact angle is nearly
. Surface tension therefore exerts an upward force when it flattens the surface to reduce its area.
Capillary action can move liquids horizontally over very large distances, but the height to which it can raise or suppress a liquid in a tube is limited by its weight. It can be shown that this height is given by
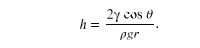
If we look at the different factors in this expression, we might see how it makes good sense. The height is directly proportional to the surface tension , which is its direct cause. Furthermore, the height is inversely proportional to tube radius—the smaller the radius
, the higher the fluid can be raised, since a smaller tube holds less mass. The height is also inversely proportional to fluid density
, since a larger density means a greater mass in the same volume. (See figure below.)
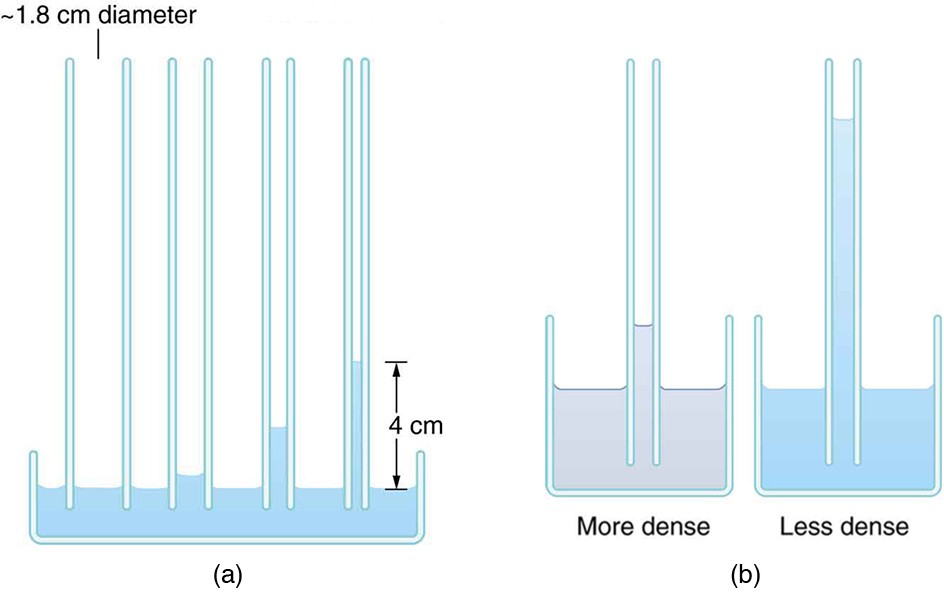
(a) Capillary action depends on the radius of a tube. The smaller the tube, the greater the height reached. The height is negligible for large-radius tubes. (b) A denser fluid in the same tube rises to a smaller height, all other factors being the same
Thermal Expansion of Solids and Liquids
The expansion of alcohol in a thermometer is one of many commonly encountered examples of thermal expansion, the change in size or volume of a given mass with temperature. Hot air rises because its volume increases, which causes the hot air’s density to be smaller than the density of surrounding air, causing a buoyant (upward) force on the hot air. The same happens in all liquids and gases, driving natural heat transfer upwards in homes, oceans, and weather systems. Solids also undergo thermal expansion. Railroad tracks and bridges, for example, have expansion joints to allow them to freely expand and contract with temperature changes.

Thermal expansion joints like these in the Auckland Harbour Bridge in New Zealand allow bridges to change length without buckling. (credit: Ingolfson, Wikimedia Commons)
First, thermal expansion is clearly related to temperature change. The greater the temperature change, the more a bimetallic strip will bend. Second, it depends on the material. In a thermometer, for example, the expansion of alcohol is much greater than the expansion of the glass containing it.
an increase in temperature implies an increase in the kinetic energy of the individual atoms. In a solid, unlike in a gas, the atoms or molecules are closely packed together, but their kinetic energy (in the form of small, rapid vibrations) pushes neighboring atoms or molecules apart from each other. This neighbor-to-neighbor pushing results in a slightly greater distance, on average, between neighbors, and adds up to a larger size for the whole body. For most substances under ordinary conditions, there is no preferred direction, and an increase in temperature will increase the solid’s size by a certain fraction in each dimension
The change in length ∆ L is proportional to length L. The dependence of thermal expansion on temperature, substance, and length is summarized in the equation
∆ L = α L ∆ T
Where ∆ L is the change in length , ∆ T is the change in temperature, and α is the coefficient of linear expansion, which varies slightly with temperature.
The below table lists representative values of the coefficient of linear expansion, which may have units of 1/0 C or 1/K. Because the size of a kelvin and a degree Celsius are the same, both and can be expressed in units of kelvins or degrees Celsius. The equation ∆ L = α L ∆ T is accurate for small changes in temperature and can be used for large changes in temperature if an average value of is used.


Thermal Expansion in Two and Three Dimensions
Objects expand in all dimensions, as illustrated in the below figure . That is, their areas and volumes, as well as their lengths, increase with temperature. Holes also get larger with temperature. If you cut a hole in a metal plate, the remaining material will expand exactly as it would if the plug was still in place. The plug would get bigger, and so the hole must get bigger too. (Think of the ring of neighboring atoms or molecules on the wall of the hole as pushing each other farther apart as temperature increases. Obviously, the ring of neighbors must get slightly larger, so the hole gets slightly larger).
For small temperature changes, the change in area ∆ A is given by
∆ A = 2 α A ∆ T
Where ∆ A is the change in area , ∆ T is the change in temperature, and α is the coefficient of linear expansion, which varies slightly with temperature
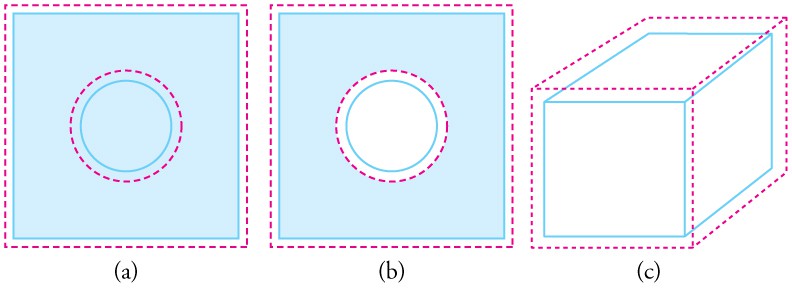
In general, objects expand in all directions as temperature increases. In these drawings, the original boundaries of the objects are shown with solid lines, and the expanded boundaries with dashed lines. (a) Area increases because both length and width increase. The area of a circular plug also increases. (b) If the plug is removed, the hole it leaves becomes larger with increasing temperature, just as if the expanding plug were still in place. (c) Volume also increases, because all three dimensions increase

In general, objects will expand with increasing temperature. Water is the most important exception to this rule. Water expands with increasing temperature (its density decreases) when it is at temperatures greater than 4oC (40oF). However, it expands with decreasing temperature when it is between +4oC and 0oC(40oF 32oF). Water is densest at +4oC. (See below graph.) Perhaps the most striking effect of this phenomenon is the freezing of water in a pond. When water near the surface cools down to 4oC it is denser than the remaining water and thus will sink to the bottom. This “turnover” results in a layer of warmer water near the surface, which is then cooled.
Eventually the pond has a uniform temperature of 4oC. If the temperature in the surface layer drops below 4oC, the water is less dense than the water below, and thus stays near the top. As a result, the pond surface can completely freeze over. The ice on top of liquid water provides an insulating layer from winter’s harsh exterior air temperatures. Fish and other aquatic life can survive in 4oC water beneath ice, due to this unusual characteristic of water. It also produces circulation of water in the pond that is necessary for a healthy ecosystem of the body of water.
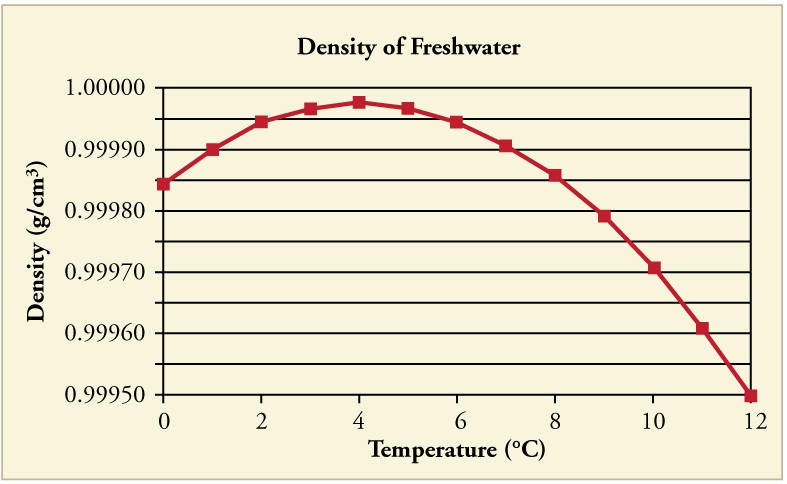
The density of water as a function of temperature. Note that the thermal expansion is actually very small. The maximum density at +4oC is only 0.0075% greater than the density at 2oC, and 0.012% greater than that at 0oC.
Thermal Stress
Thermal stress is created by thermal expansion or contraction . Thermal stress can be destructive, such as when expanding petrol ruptures a tank. It can also be useful, for example, when two parts are joined together by heating one in manufacturing, then slipping it over the other and allowing the combination to cool. Thermal stress can explain many phenomena, such as the weathering of rocks and pavement by the expansion of ice when it freezes.
Forces and pressures created by thermal stress are typically large (See below figure.)

Thermal stress contributes to the formation of potholes. credit: Editor5807, Wikimedia Commons
Power lines sag more in the summer than in the winter, and will snap in cold weather if there is insufficient slack. Cracks open and close in plaster walls as a house warms and cools. Glass cooking pans will crack if cooled rapidly or unevenly, because of differential contraction and the stresses it creates. (Pyrex® is less susceptible because of its small coefficient of thermal expansion.) Nuclear reactor pressure vessels are threatened by overly rapid cooling, and although none have failed, several have been cooled faster than considered desirable. Biological cells are ruptured when foods are frozen, detracting from their taste. Repeated thawing and freezing accentuate the damage. Even the oceans can be affected. A significant portion of the rise in sea level that is resulting from global warming is due to the thermal expansion of sea water.
Metal is regularly used in the human body for hip and knee implants. Most implants need to be replaced over time because, among other things, metal does not bond with bone. Researchers are trying to find better metal coatings that would allow metal-to-bone bonding. One challenge is to find a coating that has an expansion coefficient similar to that of metal. If the expansion coefficients are too different, the thermal stresses during the manufacturing process lead to cracks at the coating-metal interface.
Another example of thermal stress is found in the mouth. Dental fillings can expand differently from tooth enamel. It can give pain when eating ice cream or having a hot drink. Cracks might occur in the filling. Metal fillings (gold, silver, etc.) are being replaced by composite fillings (porcelain), which have smaller coefficients of expansion, and are closer to those of teeth
Heat
Work is defined as force times distance and in earlier chapters we learned that work done on an object changes its kinetic energy. We also saw in previous lessons that temperature is proportional to the (average) kinetic energy of atoms and molecules. We say that a thermal system has a certain internal energy: its internal energy is higher if the temperature is higher. If two objects at different temperatures are brought in contact with each other, energy is transferred from the hotter to the colder object until equilibrium is reached and the bodies reach thermal equilibrium (i.e., they are at the same temperature). No work is done by either object, because no force acts through a distance. The transfer of energy is caused by the temperature difference, and ceases once the temperatures are equal. These observations lead to the following definition of heat: Heat is the spontaneous transfer of energy due to a temperature difference
Heat is often confused with temperature. For example, we may say the heat was unbearable, when we actually mean that the temperature was high. Heat is a form of energy, whereas temperature is not. The misconception arises because we are sensitive to the flow of heat, rather than the temperature.
Owing to the fact that heat is a form of energy, it has the SI unit of joule (J). The calorie (cal) is a common unit of energy, defined as the energy needed to change the temperature of 1.00 g of water by 1.00oC —specifically, between 14.5oC and 15.5oC , since there is a slight temperature dependence. Perhaps the most common unit of heat is the kilocalorie (kcal), which is the energy needed to change the temperature of 1.00 kg of water by 1.00oC . Since mass is most often specified in kilograms, kilocalorie is commonly used. Food calories (given the notation Cal, and sometimes called “big calorie”) are actually kilocalories (1 Kilocalorie = 1000 calories), a fact not easily determined from package labeling.
Mechanical Equivalent of Heat
It is also possible to change the temperature of a substance by doing work. Work can transfer energy into or out of a system. This realization helped establish the fact that heat is a form of energy. James Prescott Joule (1818–1889) performed many experiments to establish the mechanical equivalent of heat—the work needed to produce the same effects as heat transfer. In terms of the units used for these two terms, the best modern value for this equivalence is
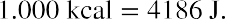
We consider this equation as the conversion between two different units of energy
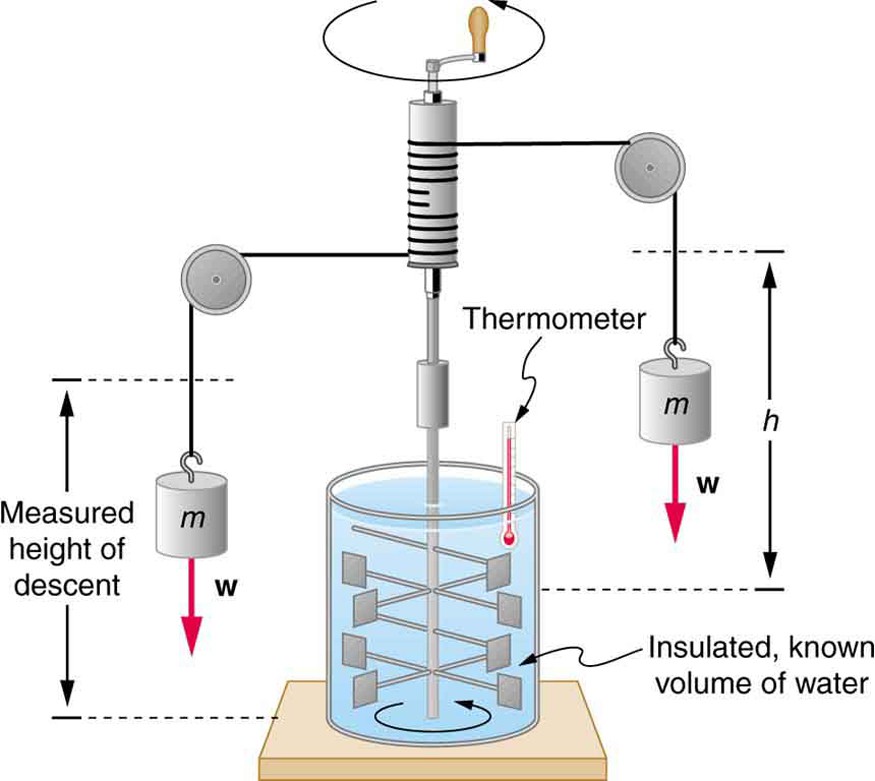
Schematic depiction of Joule’s experiment that established the equivalence of heat and work
The figure above shows one of Joule’s most famous experimental setups for demonstrating the mechanical equivalent of heat. It demonstrated that work and heat can produce the same effects, and helped establish the principle of conservation of energy. Gravitational potential energy (PE) (work done by the gravitational force) is converted into kinetic energy (KE), and then randomized by viscosity and turbulence into increased average kinetic energy of atoms and molecules in the system, producing a temperature increase. His contributions to the field of thermodynamics were so significant that the SI unit of energy was named after him.
Heat added or removed from a system changes its internal energy and thus its temperature. Such a temperature increase is observed while cooking. However, adding heat does not necessarily increase the temperature. An example is melting of ice; that is, when a substance changes from one phase to another. Work done on the system or by the system can also change the internal energy of the system. Joule demonstrated that the temperature of a system can be increased by stirring. If an ice cube is rubbed against a rough surface, work is done by the frictional force. A system has a well-defined internal energy, but we cannot say that it has a certain “heat content” or “work content”. We use the phrase “heat transfer” to emphasize its nature.
Temperature Change and Heat Capacity
One of the major effects of heat transfer is temperature change: heating increases the temperature while cooling decreases it. We assume that there is no phase change and that no work is done on or by the system. Experiments show that the transferred heat depends on three factors—the change in temperature, the mass of the system, and the substance and phase of the substance.
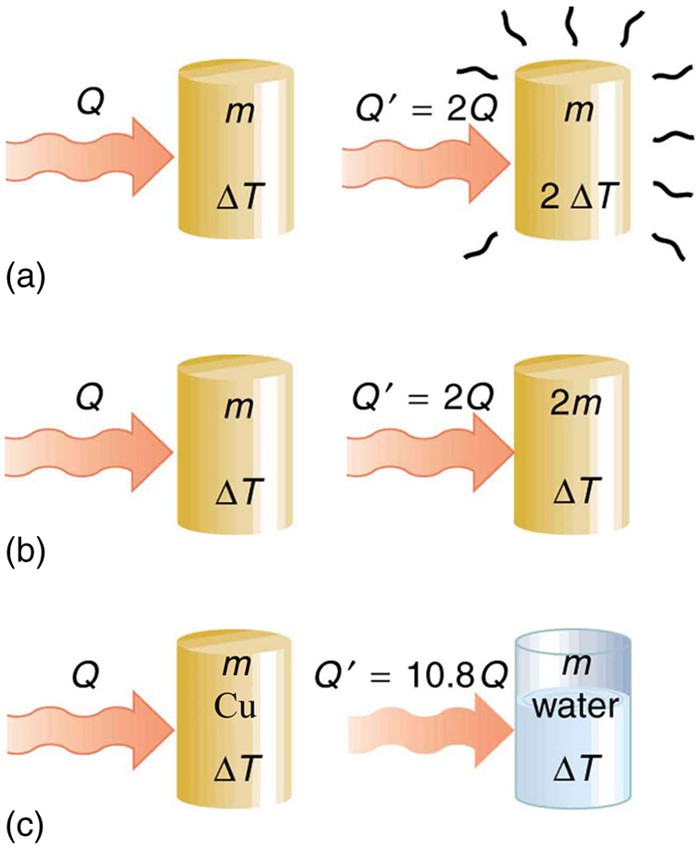
The heat Q transferred to cause a temperature change depends on the magnitude of the temperature change, the mass of the system, and the substance and phase involved. (a) The amount of heat transferred is directly proportional to the temperature change. To double the temperature change of a mass m, you need to add twice the heat. (b) The amount of heat transferred is also directly proportional to the mass. To cause an equivalent temperature change in a doubled mass, you need to add twice the heat. (c) The amount of heat transferred depends on the substance and its phase. If it takes an amount Q of heat to cause a temperature change ∆T in a given mass of copper, it will take 10.8 times that amount of heat to cause the equivalent temperature change in the same mass of water assuming no phase change in either substance
The dependence on temperature change and mass are easily understood. Owing to the fact that the (average) kinetic energy of an atom or molecule is proportional to the absolute temperature, the internal energy of a system is proportional to the absolute temperature and the number of atoms or molecules. Owing to the fact that the transferred heat is equal to the change in the internal energy, the heat is proportional to the mass of the substance and the temperature change. The transferred heat also depends on the substance so that, for example, the heat necessary to raise the temperature is less for alcohol than for water. For the same substance, the transferred heat also depends on the phase (gas, liquid, or solid).

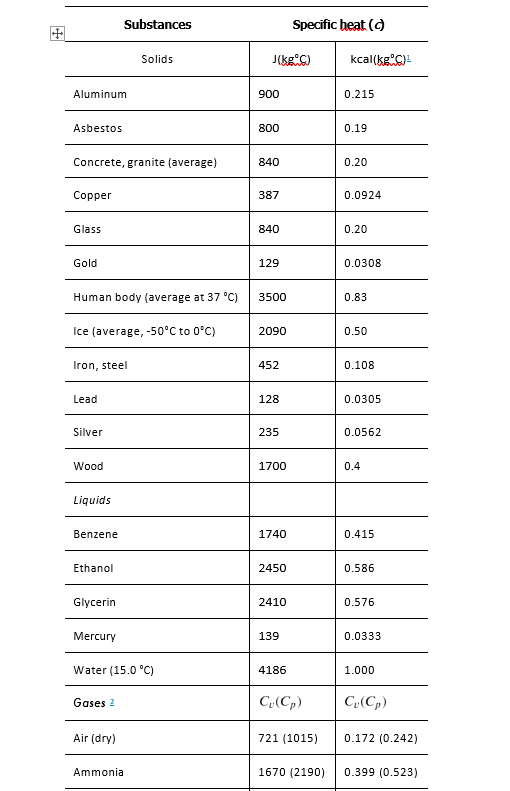
Values of specific heat must generally be looked up in tables, because there is no simple way to calculate them. In general, the specific heat also depends on the temperature. The table below lists representative values of specific heat for various substances. Except for gases, the temperature and volume dependence of the specific heat of most substances is weak. We see from this table that the specific heat of water is five times that of glass and ten times that of iron, which means that it takes five times as much heat to raise the temperature of water the same amount as for glass and ten times as much heat to raise the temperature of water as for iron. In fact, water has one of the largest specific heats of any material, which is important for sustaining life on Earth.
Calorimetry
One technique we can use to measure the amount of heat involved in a physical or chemical process is known as calorimetry. Calorimetry is used to measure amounts of heat transferred to or from a substance. To do so, the heat is exchanged with a calibrated object (calorimeter). The temperature change measured by the calorimeter is used to derive the amount of heat transferred by the process under study. The measurement of heat transfer using this approach requires the definition of a system (the substance or substances undergoing the chemical or physical change) and its surroundings (all other matter, including components of the measurement apparatus, that serve to either provide heat to the system or absorb heat from the system).
A calorimeter is a device used to measure the amount of heat involved in a chemical or physical process. For example, when an exothermic reaction occurs in solution in a calorimeter, the heat produced by the reaction is absorbed by the solution, which increases its temperature. When an endothermic reaction occurs, the heat required is absorbed from the thermal energy of the solution, which decreases its temperature (Figure below). The temperature change, along with the specific heat and mass of the solution, can then be used to calculate the amount of heat involved in either case.
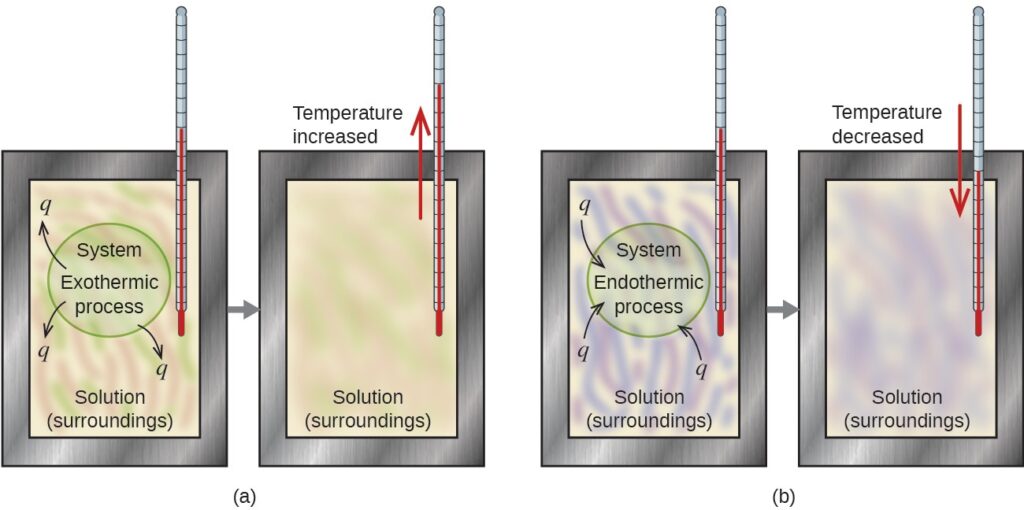
In a calorimetric determination, either (a) an exothermic process occurs and heat, q, is negative, indicating that thermal energy is transferred from the system to its surroundings, or (b) an endothermic process occurs and heat, q, is positive, indicating that thermal energy is transferred from the surroundings to the system
Calorimetry measurements are important in understanding the heat transferred in reactions involving everything from microscopic proteins to massive machines .
Consider a simpler example that illustrates the core idea behind calorimetry. Suppose we initially have a high-temperature substance, such as a hot piece of metal (M), and a low-temperature substance, such as cool water (W). If we place the metal in the water, heat will flow from M to W. The temperature of M will decrease, and the temperature of W will increase, until the two substances have the same temperature—that is, when they reach thermal equilibrium (Figure below ). If this occurs in a calorimeter, ideally all of this heat transfer occurs between the two substances, with no heat gained or lost by either its external environment
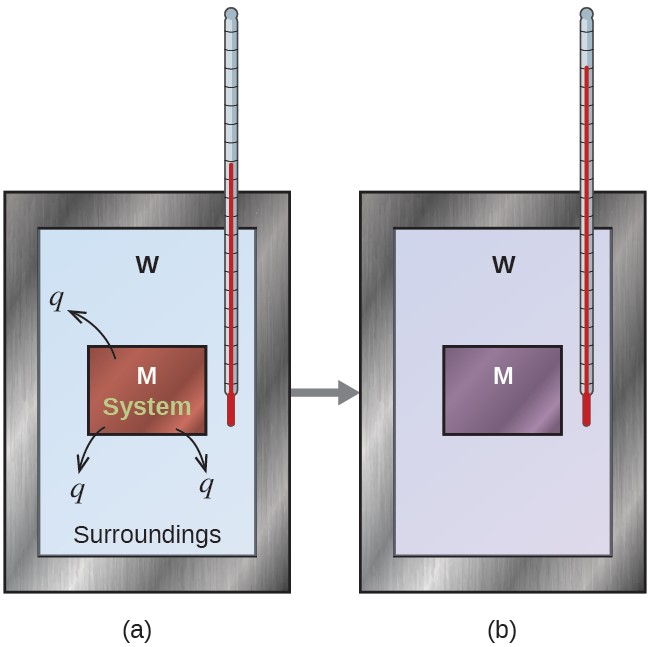
In a simple calorimetry process, (a) heat, q, is transferred from the hot metal, M, to the cool water, W, until (b) both are at the same temperature
Under these ideal circumstances, the net heat change is zero

This relationship can be rearranged to show that the heat gained by substance M is equal to the heat lost by substance W:
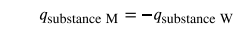
The magnitude of the heat (change) is therefore the same for both substances, and the negative sign merely shows that qsubstance M and qsubstance W are opposite in direction of heat flow (gain or loss) but does not indicate the arithmetic sign of either q value (that is determined by whether the matter in question gains or loses heat, per definition). In the specific situation described, qsubstance M is a negative value and qsubstance W is positive, since heat is transferred from M to W.
