Kinematics is defined as the study of motion without considering its causes. The word “kinematics” comes from a Greek term meaning motion and is related to other English words such as “cinema” (movies) and “kinesiology” (the study of human motion). In one-dimensional kinematics we will study only the motion of a ball, for example, without worrying about what forces cause or change its motion. Such considerations come in other chapters. In this chapter, we examine the simplest type of motion—namely, motion along a straight line, or one-dimensional motion.

Position

In order to describe the motion of an object, you must first be able to describe its position—where it is at any particular time. More precisely, you need to specify its position relative to a convenient reference frame. Earth is often used as a reference frame, and we often describe the position of an object as it relates to stationary objects in that reference frame. For example, a rocket launch would be described in terms of the positionof the rocket with respect to the Earth as a whole, while a professor’s positioncould be described in terms of where she is in relation to the nearby white board.  In other cases, we use reference frames that are not stationary but are in motionrelative to the Earth. To describe the position of a person in an airplane, for example, we use the airplane, not the Earth, as the reference frame.  

Displacement

If an object moves relative to a reference frame (for example, if a professor moves to the right relative to a white board or a passenger moves toward the rear of an airplane), then the object’s position changes. This change in position is known as displacement. The word “displacement” implies that an object has moved, or has been displaced.

Definition: 

DISPLACEMENT

Displacement is the change in position of an object:

Δx=xf−x0,

where Δx is displacement , x_f is the final position and x ₀ is the initial position

In this text the upper case Greek letter Δ always means “change in” whatever quantity follows it; thus, Δx means change in position

We can find displacement by subtracting initial position X₀ from the final position X_f

Note that the SI unit for displacement is the meter (m), but sometimes kilometres, miles, feet, and other units of length are used. Keep in mind that when units other than the meter are used in a problem, you may need to convert them into meters to complete the calculation.

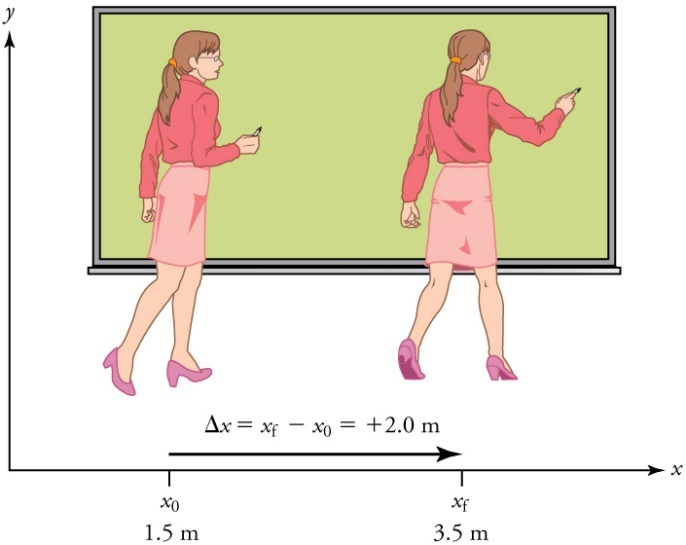
A professor paces left and right while lecturing. Her position relative to Earth is given by x. The +2.0 m displacement of the professor relative to Earth is represented by an arrow pointing to the right.

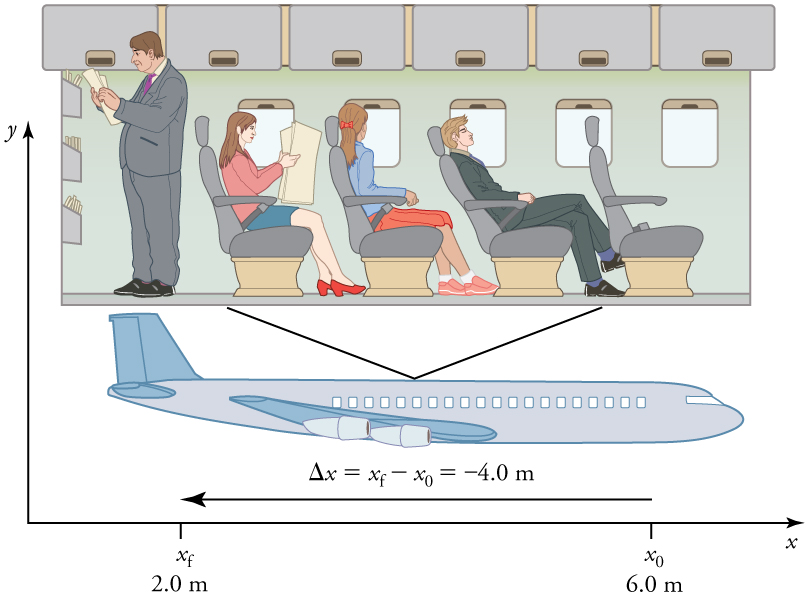
A passenger moves from his seat to the back of the plane. His location relative to the airplane is given by x. The −4.0 m displacement of the passenger relative to the plane is represented by an arrow toward the rear of the plane. Notice that the arrow representing his displacement is twice as long as the arrow representing the displacement of the professor (he moves twice as far)  

Note that displacement has a direction as well as a magnitude. The professor’s displacement is 2.0 m to the right, and the airline passenger’s displacement is 4.0 m toward the rear. In one-dimensional motion, direction can be specified with a plus or minus sign. When you begin a problem, you should select which direction is positive (usually that will be to the right or up, but you are free to select positive as being any direction).

The professor’s initial position is X₀ =1.5 m and her final position is X_f =3.5 m . Thus her displacement is

Δx=Xf−X0=3.5 m−1.5 m=+2.0 m.

In this coordinate system, motion to the right is positive, whereas motion to the left is negative.

Similarly, the airplane passenger’s initial position is X0=6.0 m and his final position is Xf=2.0m and hence his displacement is

Δx=Xf−X0=2.0 m−6.0 m=−4.0 m.

His displacement is negative because his motion is toward the rear of the plane, or in the negative x direction in our coordinate system.

Distance

Although displacement is described in terms of direction, distance is not. 

Distance is defined to be the magnitude or size of displacement between two positions. Note that the distance between two positions is not the same as the 

distance travelled between them. 

Distance travelled is the total length of the path traveled between two positions. 

Distancehas no direction and, thus, no sign. For example, the distance

 the professor walks is 2.0 m. The distance the airplane passenger walks is 4.0 m.

MISCONCEPTION ALERT: 

DISTANCE TRAVELED VS. MAGNITUDE OF DISPLACEMENT

It is important to note that the distance traveled, however, can be greater than the magnitude of the displacement (by magnitude, we mean just the size of the displacement without regard to its direction; that is, just a number with a unit). For example, the professor could pace back and forth many times, perhaps walking a distance of 150 m during a lecture, yet still end up only 2.0 m to the right of her starting point. In this case her displacement would be +2.0 m, the magnitude of her displacement would be 2.0 m, but the distance she travelled would be 150 m.

In kinematics we nearly always deal with displacement and magnitude of displacement, and almost never with distance travelled. One way to think about this is to assume you marked the start of the motion and the end of the motion. The 

Displacement is simply the difference in the position of the two marks and is independent of the path taken in traveling between the two marks. The 

distance travelled, however, is the total length of the path taken between the two marks.

Exercise 

A cyclist rides 3 km west and then turns around and rides 2 km east. (a) What is her displacement? (b) What distance does she ride? (c) What is the magnitude of her displacement?

Answer

The rider’s displacement is .

a) Δx=Xf−X0 = 2 – 3 = -1  (The displacement is negative because we take east to be positive and west to be negative.)

 (b) The distance traveled is 3 km + 2 km = 5 km.

(c) The magnitude of the displacement is 1 km

Vectors, Scalars, and Coordinate Systems

What is the difference between distance and displacement?

Whereas displacement is defined by both direction and magnitude, distance is defined only by magnitude. Displacement is an example of a vector quantity. Distance is an example of a scalar quantity.

A vector is any quantity with both magnitude and direction. Other examples of vectors include a velocity of 90 km/h east and a force of 500 newtons straight down. The direction of a vector in one-dimensional motion is given simply by a plus (+) or minus (−) sign. Vectors are represented graphically by arrows. An arrow used to represent a vector has a length proportional to the vector’s magnitude (e.g., the larger the magnitude, the longer the length of the vector) and points in the same direction as the vector. Some physical quantities, like distance, either have no direction or none is specified.

A scalar is any quantity that has a magnitude, but no direction. For example, a 20ºC temperature, the 250 kilocalories (250 Calories) of energy in a candy bar, a 90 km/h speed limit, a person’s 1.8 m height, and a distance of 2.0 m are all scalars—quantities with no specified direction. Note, however, that a scalar can be negative, such as a −20ºC temperature. In this case, the minus sign indicates a point on a scale rather than a direction. Scalars are never represented by arrows.

Coordinate Systems for One-Dimensional Motion

In order to describe the direction of a vector quantity, you must designate a coordinate system within the reference frame. For one dimensional motion, this is a simple coordinate system consisting of a one-dimensional coordinate line. In general, when describing horizontal motion, motion to the right is usually considered positive, and motion to the left is considered negative. With vertical motion, motion up is usually positive and motion down is negative. In some cases, however, as with the jet in Figure , it can be more convenient to switch the positive and negative directions. For example, if you are analyzing the motion of falling objects, it can be useful to define downwards as the positive direction. If people in a race are running to the left, it is useful to define left as the positive direction. It does not matter as long as the system is clear and consistent. Once you assign a positive direction and start solving a problem, you cannot change it. Figure :

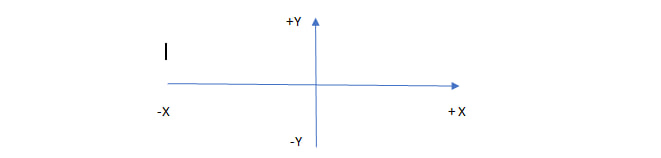
It is usually convenient to consider motion upward or to the right as positive (+) and motion downward or to the left as negative (−).

Time, Velocity, and Speed :

There is more to motion than distance and displacement. Questions such as, “How long does a foot race take?” and “What was the runner’s speed?” cannot be answered without an understanding of other concepts. In this section we add definitions of time, velocity, and speed to expand our description of motion.

Time

The most fundamental physical quantities are defined by how they are measured. This is the case with time. Every measurement of time involves measuring a change in some physical quantity. It may be a number on a digital clock, a heartbeat, or the position of the Sun in the sky. In physics, the definition of time is simple—time is change, or the interval over which change occurs. It is impossible to know that time has passed unless something changes. The amount of time or change is calibrated by comparison with a standard. The SI unit for time is the second, abbreviated s. We might, for example, observe that a certain pendulum makes one full swing every 0.75 s. We could then use the pendulum to measure time by counting its swings or, of course, by connecting the pendulum to a clock mechanism that registers time on a dial. This allows us to not only measure the amount of time, but also to determine a sequence of events.

How does time relate to motion? We are usually interested in elapsed time for a particular motion, such as how long it takes an airplane passenger to get from his seat to the back of the plane. To find elapsed time, we note the time at the beginning and end of the motion and subtract the two. For example, a lecture may start at 11:00 A.M. and end at 11:50 A.M., so that the elapsed time would be 50 min.

Elapsed time Δt is the difference between the ending time and beginning time,

Δt = t_f – t₀ , where

Where Δt is the change in time or elapsed time, is the time at the end of the motion, and t₀ is the time at the beginning of the motion.

Velocity

Your notion of velocity is probably the same as its scientific definition. You know that if you have a large displacement in a small amount of time you have a large velocity, and that velocity has units of distance divided by time, such as miles per hour or kilometres per hour.

Average velocity is displacement (change in position) divided by the time of travel,

ṽ =  Δx / Δt  = (X_f −X₀) /  (t_f −t₀)

where ṽ  is the average (indicated by the bar over the v) velocity, Δx is the change in position (or displacement), and X_f  and X₀ are the final and beginning positions at times t_f and t₀  respectively

Notice that this definition indicates that velocity is a vector because displacement is a vector. It has both magnitude and direction. The SI unit for velocity is meters per second or m/s, but many other units, such as km/h, mi/h (also written as mph), and cm/s, are in common use.

Suppose, for example, an airplane passenger took 5 seconds to move −4 m (the negative sign indicates that displacement is toward the back of the plane). His average velocity would be

ṽ =  Δx / Δt  = (-4m)/5s = -0.8 m/s

The average velocity of an object does not tell us anything about what happens to it between the starting point and ending point, however. For example, we cannot tell from average velocity whether the airplane passenger stops momentarily or backs up before he goes to the back of the plane. To get more details, we must consider smaller segments of the trip over smaller time intervals.

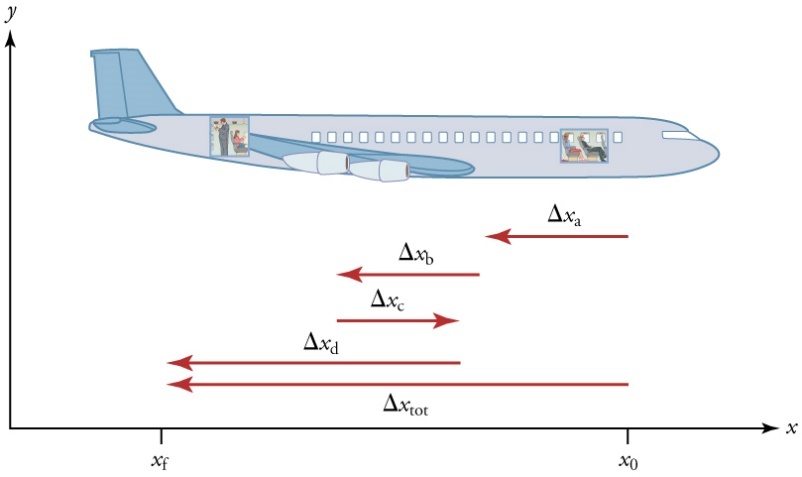
The smaller the time intervals considered in a motion, the more detailed the information. When we carry this process to its logical conclusion, we are left with an infinitesimally small interval. Over such an interval, the average velocity becomes the instantaneous velocity or the velocity at a specific instant. A car’s speedometer, for example, shows the magnitude (but not the direction) of the instantaneous velocityof the car. (Police give tickets based on instantaneous velocity, but when calculating how long it will take to get from one place to another on a road trip, you need to use average velocity.) 

Instantaneous velocity v is the average velocity at a specific instant in time (or over an infinitesimally small timeinterval).

Speed

In everyday language, most people use the terms “speed” and “velocity” interchangeably. In physics, however, they do not have the same meaning and they are distinct concepts. One major difference is that speed has no direction. Thus speed is a scalar . Just as we need to distinguish between instantaneous velocity and average velocity, we also need to distinguish between instantaneous speed and average speed

Instantaneous speed is the magnitude of instantaneous velocity . For example, suppose the airplane passenger at one instant had an instantaneous velocity  of −3.0 m/s (the minus meaning toward the rear of the plane). At that same time  his instantaneous speed was 3.0 m/s. Or suppose that at one time during a shopping trip your instantaneous velocity is 40 km/h due north. Your instantaneous speed at that instant would be 40 km/h—the same magnitude but without a direction. 

Average speed , however, is very different from average velocity.  Average speed  is the distance travelled  divided by elapsed time .

We have noted that distance travelled  can be greater than displacement. So average speedcan be greater than average velocity , which is displacement  divided by time . For example, if you drive to a store and return home in half an hour, and your car’s odometer shows the total distance travelled  was 6 km, then your average speed  was 12 km/h. Your average velocity , however, was zero, because your displacement  for the round trip is zero. (Displacement is change in position  and, thus, is zero for a round trip.) Thus average speed is not simply the magnitude of average velocity

Another way of visualizing the motion  of an object is to use a graph. A plot of position or of velocity as a function of time  can be very useful. For example, for this trip to the store, the position , velocity, and speed-vs.-time graphs are displayed (Note that these graphs depict a very simplified model of the trip. We are assuming that speed is constant during the trip, which is unrealistic given that we’ll probably stop at the store. But for simplicity’s sake, we will model it with no stops or changes in speed. We are also assuming that the route between the store and the house is a perfectly straight line.)

.

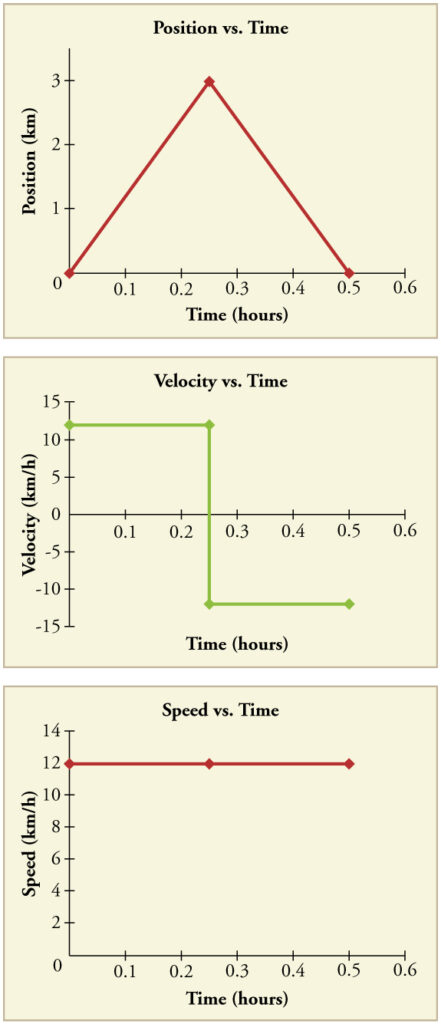
Position vs. time , velocity vs. time, and speed vs. time on a trip. Note that the velocity for the return trip is negative.

Acceleration :

In everyday conversation, to accelerate means to speed up. The accelerator in a car can in fact cause it to speed up. The greater the acceleration, the greater the change in velocity over a given time . The formal definition of 

Acceleration is consistent with these notions, but more inclusive.

AVERAGE ACCELERATION

Average Acceleration is the rate at which velocity changes,

ặ=Δv / Δt=(V_f−V₀) / (T_f−T₀)

where ặ  is average acceleration ,V is velocity, and T is time

Because acceleration is velocity in m/s divided by time  in s, the SI units for acceleration are m/s ²   (meters per second  squared)

Recall that velocity is a vector —it has both magnitude and direction. This means that a change in velocity can be a change in magnitude (or speed), but it can also be a change in direction. For example, if a car turns a corner at constant speed, it is accelerating because its direction is changing. The quicker you turn, the greater the acceleration. So there is an Acceleration when velocity changes either in magnitude (an increase or decrease in speed) or in direction, or both.

ACCELERATION AS A VECTOR

Acceleration is a  vector in the same direction as the change in velocity, Δv. Since velocity is a vector , it can change either in magnitude or in direction. Acceleration  is therefore a change in either speed or direction, or both. Keep in mind that although acceleration  is in the direction of the change in velocity, it is not always in the direction of motion

. If acceleration  is in a direction opposite to the direction of motion , the object slows down.

Problem :

A racehorse coming out of the gate accelerates from rest to a velocity of 15.0 m/s due west in 1.80 s. What is its average acceleration ?

First we draw a sketch and assign a coordinate system to the problem. This is a simple problem, but it always helps to visualize it. Notice that we assign east as positive and west as negative. Thus, in this case, we have negative velocity.

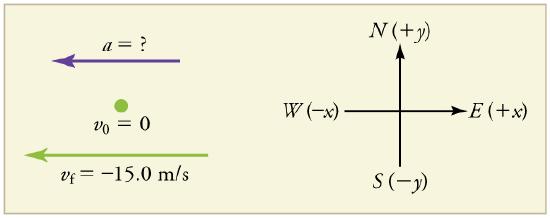
We can solve this problem by identifying Δv and Δt from the given information and then calculating the average acceleration directly from the equation

ặ=Δv / Δt=(V_f−V₀) / (T_f−T₀)

We know that

V₀=0, V_f =−15.0 m/s (the negative sign indicates direction toward the west), Δt=1.80 s

Since the horse is going from zero to −15.0 m/s, its change in velocity equals its final velocity: Δv=v_f=−15.0 m/s

Substituting the values , we  get

ặ  = (−15.0 m/s) / 1.80 s= −8.33 m/s²

Falling Objects

Falling objects form an interesting class of motion problems. For example, we can estimate the depth of a vertical mine shaft by dropping a rock into it and listening for the rock to hit the bottom. By applying the kinematics developed so far to falling objects, we can examine some interesting situations and learn much about gravity in the process.

Gravity

The most remarkable and unexpected fact about falling objects is that, if air resistance and friction are negligible, then in a given location all objects fall toward the center of Earth with the same constant acceleration, independent of their mass. This experimentally determined fact is unexpected, because we are so accustomed to the effects of air resistance and friction that we expect light objects to fall slower than heavy ones.

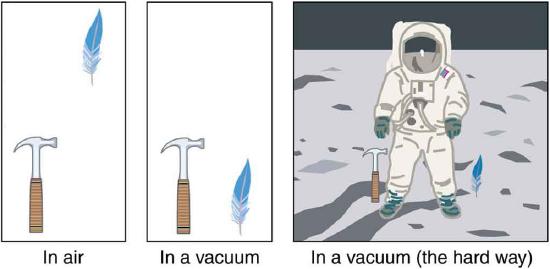
In the real world, air resistance can cause a lighter object to fall slower than a heavier object of the same size. A tennis ball will reach the ground after a hard baseball dropped at the same time . (It might be difficult to observe the difference if the height is not large.) Air resistance opposes the motion of an object through the air, while friction  between objects—such as between clothes and a laundry chute or between a stone and a pool into which it is dropped—also opposes motion between them. For the ideal situations of these first few chapters, an object falling without air resistance or friction  is defined to be in free-fall . The forceof gravity causes objects to fall toward the center of Earth. The acceleration of free-falling objects is therefore called the acceleration due to gravity . The acceleration due to gravity is constant, which means we can apply the kinematics equations to any falling object where air resistance and friction are negligible. This opens a broad class of interesting situations to us. The acceleration due to gravity is so important that its magnitude is given its own symbol, g. It is constant at any given location on Earth and has the average value

g=9.80 m/s²

The direction of the acceleration due to gravity  is downward (towards the center of Earth). In fact, its direction defines what we call vertical. Note that whether the acceleration a in the kinematic equations has the Value +g or −g depends on how we define our coordinate system . If we define the upward direction as positive, then a=−g=−9.80 m/s² , and if we define the downward direction as positive, then a=g=9.80 m/s²

KINEMATIC EQUATIONS FOR OBJECTS IN FREE FALL :

V=V₀−gt

y=y₀+v₀ t−1/2(gt²)

v²=(v₀)²−2g(y−y₀)

Example problem :

A person standing on the edge of a high cliff throws a rock straight up with an initial velocity of 13.0 m/s. The rock misses the edge of the cliff as it falls back to earth. Calculate the position  and velocity of the rock 1.00 s, 2.00 s, and 3.00 s after it is thrown, neglecting the effects of air resistance .

Solution :

Draw a sketch

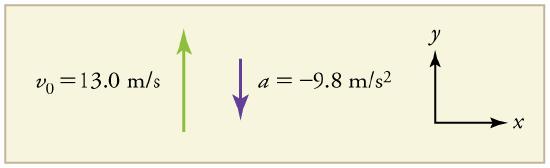
We are asked to determine the position y at various times. It is reasonable to take the initial position y₀ to be zero. This problem involves one-dimensional Motion  in the vertical direction. We use plus and minus signs to indicate direction, with up being positive and down negative. Since up is positive, and the rock is thrown upward, the initial velocity must be positive too. The acceleration due to gravity  is downward, so a is negative. It is crucial that the initial velocity and the acceleration due to gravity  have opposite signs. Opposite signs indicate that the acceleration due to gravity  opposes the nitial motion and will slow and eventually reverse it.

Since we are asked for values of position  and velocity at three times, we will refer to these as y₁ and v₁ ; y₂ and v₂; and y ₃ and v₃

Solution for Position y₁ :

We know that y₀=0; v₀=13.0 m/s; a=−g=−9.80 m/s² and t=1.00 s.

We need to Identify the best equation to use. We will use 

y=y₀+v₀ t−1/2(gt²)

which is the value we want to find.

Substituting the known values and solve for y1

y1=0+(13.0 m/s)(1.00 s) – 1/ 2(−9.80 m/s2)(1.00 s)² =8.10 m

Solution for Velocity V₁ :

Given that 

y₀=0;  v₀=13.0 m/s;  a=−g=−9.80 m/s²

We also know from the solution above that y1=8.10 m

The best equation to use is v=v₀−gt

 Where (−g )= gravitational acceleration

Substituting the values , we get  

V₁=v₀ −gt=13.0 m/s−(9.80 m/s²)(1.00 s)=3.20 m/s

Solution for Remaining Times

The procedures for calculating the position and velocity att = 2.00 s and 3.00 s are the same as those above. The results are summarized in the Table below :

Time , t	Position , y	Velocity, v
1.00 s	8.10 m	3.20 m
2.00 s	6.40 m	−6.60 m
3.00 s	−5.10m	−16.4 m

Centripetal Acceleration :

We defined acceleration  as a change in velocity, either in its magnitude or in its direction, or both. When an object moves along a circular path, the direction of its velocity changes constantly, so there is always an associated acceleration, even if the speed of the object is constant. You experience this acceleration  yourself when you turn a corner in your car. What you notice is a sideways acceleration  because you and the car are changing direction. The sharper the curve and the greater your speed, the more noticeable this acceleration  will become. In this section we briefly examine the direction and magnitude of that acceleration.

The below image shows an object moving in a circular path at constant speed, called uniform circular motion . The direction of the instantaneous velocity  is shown at two points along the path. Acceleration  is in the direction of the change in velocity, which points directly toward the center of rotation (the center of the circular path). This pointing is shown with the vector diagram in the figure. We call the acceleration of an object moving in uniform circular motion  (resulting from a net external force) the centripetal acceleration (a_c ) – centripetal means “toward the center” or “center seeking.”

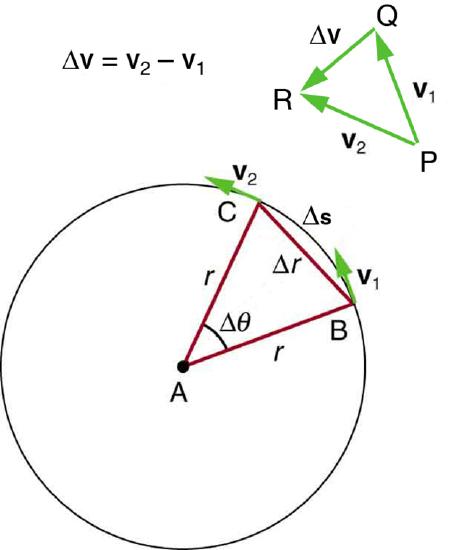
The directions of the velocity of an object at two different points are shown, and the change in velocity Δv is seen to point directly toward the center of curvature. (See small inset.) Because ac=Δv/Δt , the acceleration is also toward the center; ac is called centripetal acceleration. (For small time differences, Δθ is very small, and the arc length Δs is approximately equal to the chord length Δr)

The direction of centripetal acceleration is toward the center of curvature, but what is its magnitude? If we use the geometry shown in the above Figure along with some kinematics equations, we can obtain

ac=v² / r

which is the acceleration of an object in a circle of radius r at a speed v.

We see in the above Equation that centripetal acceleration is greater at high speeds and in sharp curves (smaller radius), as you have noticed when driving a car. But it is a bit surprising that ac is proportional to speed squared, implying, for example, that it is four times as hard to take a curve at 100 km/h than at 50 km/h. A sharp corner has a small radius, so that a_c is greater for tighter turns .

The unit of centripetal acceleration is m/s²

Take Quiz