What do a falling apple and the orbit of the moon have in common? You will learn in this chapter that each is caused by gravitational force. The motion of all celestial objects, in fact, is determined by the gravitational force, which depends on their mass and separation.

Johannes Kepler discovered three laws of planetary motion that all orbiting planets and moons follow. Years later, Isaac Newton found these laws useful in developing his law of universal gravitation. This law relates gravitational force to the masses of objects and the distance between them.

Kepler’s Laws of Planetary Motion

Hundreds of artificial satellites orbit Earth together with thousands of pieces of debris. The moon’s orbit around Earth has intrigued humans from time immemorial. The orbits of planets, asteroids, meteors, and comets around the sun are no less interesting. If we look farther, we see almost unimaginable numbers of stars, galaxies, and other celestial objects orbiting one another and interacting through gravity.

All these motions are governed by gravitational force. The orbital motions of objects in our own solar system are simple enough to describe with a few fairly simple laws. The orbits of planets and moons satisfy the following two conditions:

• The mass of the orbiting object, m, is small compared to the mass of the object it orbits, M.
• The system is isolated from other massive objects.

Based on the motion of the planets about the sun, Kepler devised a set of three classical laws, called Kepler’s laws of planetary motion, that describe the orbits of all bodies satisfying these two conditions:

1. The orbit of each planet around the sun is an ellipse with the sun at one focus.
2. Each planet moves so that an imaginary line drawn from the sun to the planet sweeps out equal areas in equal times.
3. The ratio of the squares of the periods of any two planets about the sun is equal to the ratio of the cubes of their average distances from the sun.

Kepler’s First Law

The orbit of each planet about the sun is an ellipse with the sun at one focus, as shown in the below figure . The planet’s closest approach to the sun is called aphelion and its farthest distance from the sun is called perihelion

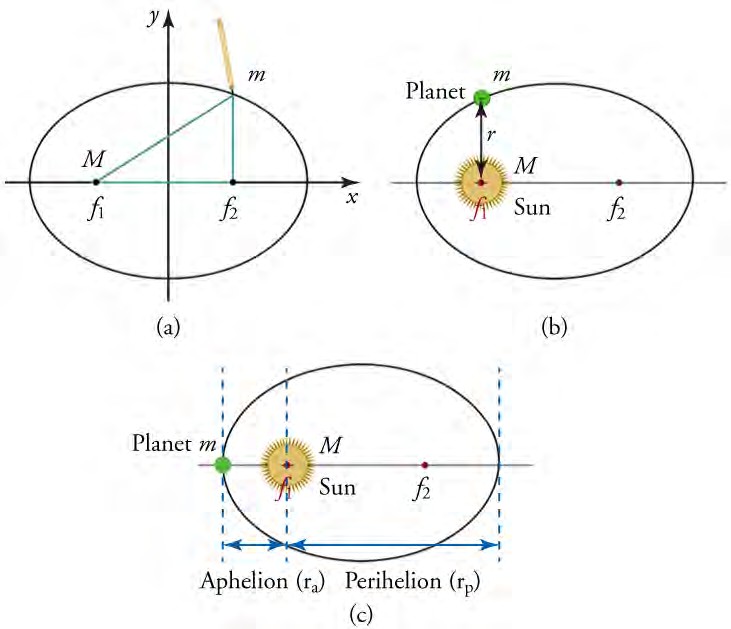
a) An ellipse is a closed curve such that the sum of the distances from a point on the curve to the two foci (f₁ and f₂) is constant.

(b) For any closed orbit, m follows an elliptical path with M at one focus.

(c) The aphelion (ra) is the closest distance between the planet and the sun, while the perihelion (rp) is the farthest distance from the sun

Hence , If you know the aphelion (r_a) and perihelion (r_p) distances, then you can calculate the semi-major axis (a) and semi-minor axis (b).

a = (r_a + r_p)/2

b = √r_ar_p

Kepler’s Second Law

Each planet moves so that an imaginary line drawn from the sun to the planet sweeps out equal areas in equal times, as shown in the below figure

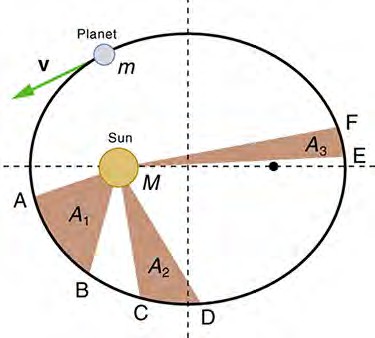
The shaded regions have equal areas. The time for m to go from A to B is the same as the time to go from C to D and from E to F. The mass m moves fastest when it is closest to M. Kepler’s second law was originally devised for planets orbiting the sun, but it has broader validity.

Kepler’s Third Law

The ratio of the periods squared of any two planets around the sun is equal to the ratio of their average distances from the sun cubed. In equation form, this is

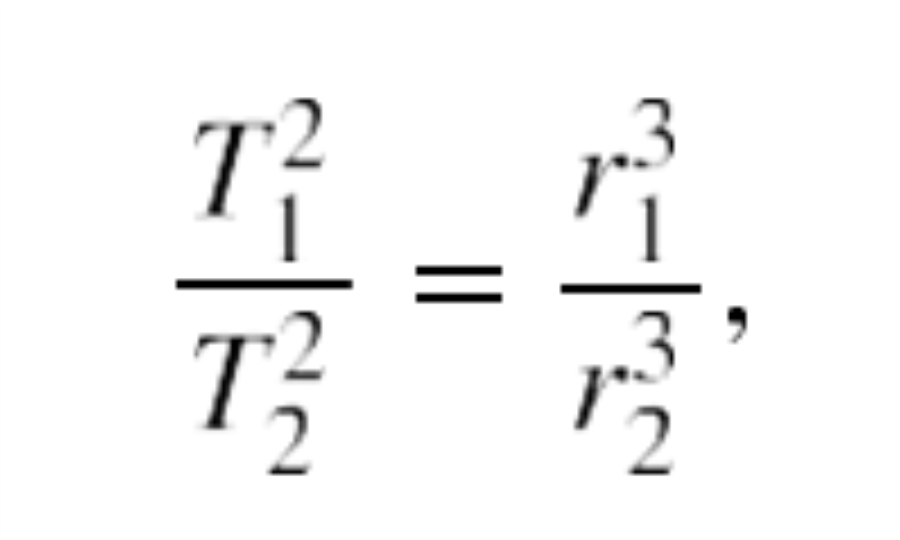
where T is the period (time for one orbit) and r is the average distance (also called orbital radius). This equation is valid only for comparing two small masses orbiting a single large mass. Most importantly, this is only a descriptive equation; it gives no information about the cause of the equality.

Newton’s Universal Law of Gravitation :

Newton was the first to propose an exact mathematical form and to use that form to show that the motion of heavenly bodies should be conic sections—circles, ellipses, parabolas, and hyperbolas. This theoretical prediction was a major triumph. It had been known for some time that moons, planets, and comets follow such paths, but no one had been able to propose an explanation of the mechanism that caused them to follow these paths and not others.

The gravitational force between two bodies  is always attractive and depends on the masses involved and the distance between them. Expressed in modern language, Newton’s universal law of gravitation states that every object in the universe attracts every other object with a force that is directed along a line joining them. The force is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. This attraction is illustrated by the below figure

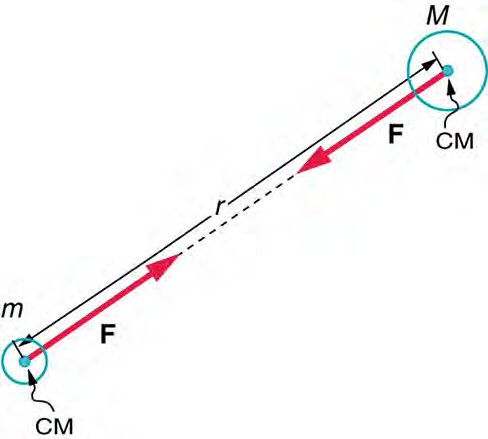
Gravitational attraction is along a line joining the centers of mass (CM) of the two bodies. The magnitude of the force on each body is the same, consistent with Newton’s third law (action-reaction).

For two bodies having masses m and M with a distance r between their centers of mass, the equation for Newton’s universal law of gravitation is

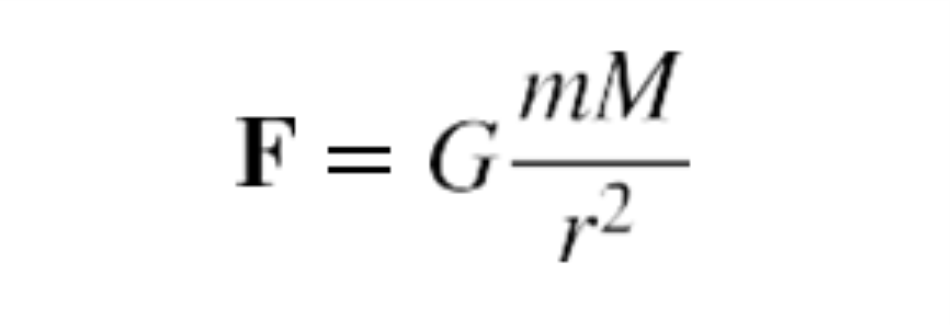
where F is the magnitude of the gravitational force and G is a proportionality factor called the gravitational constant. G is a universal constant, meaning that it is thought to be the same everywhere in the universe. It has been measured experimentally to be

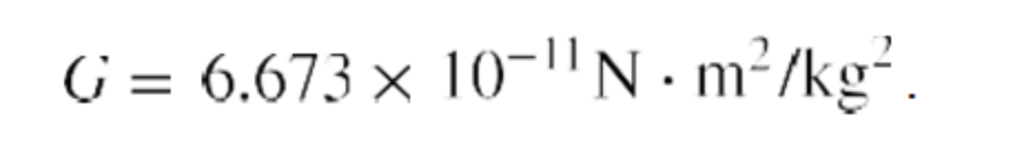
If a person has a mass of 60.0 kg, what would be the force of gravitational attraction on him at Earth’s surface? G is given above, Earth’s mass M is 5.97 × 1024 kg, and the radius r of Earth is 6.38 × 106 m. Putting these values into Newton’s universal law of gravitation gives

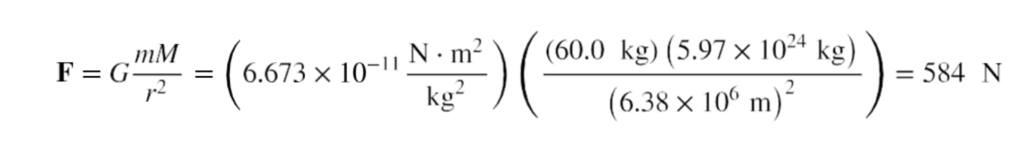
We can check this result with the relationship:

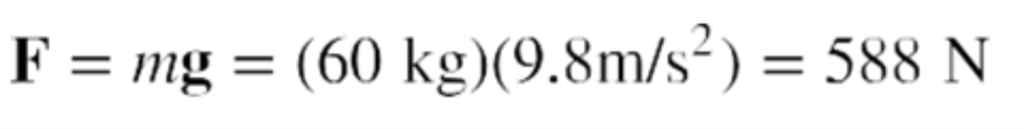
You may remember that g, the acceleration due to gravity, is another important constant related to gravity. By substituting g for a in the equation for Newton’s second law of motion we get F = mg. Combining this with the equation for universal gravitation gives

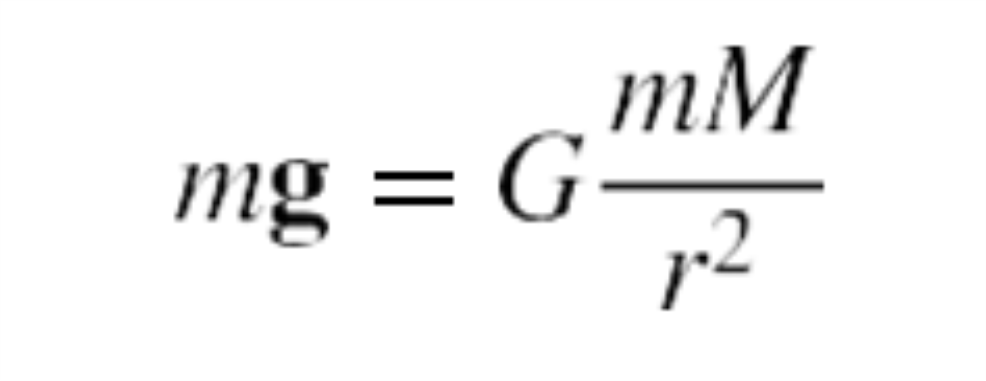
Cancelling the mass m on both sides of the equation and filling in the values for the gravitational constant and mass and radius of the Earth, gives the value of g, which may look familiar.

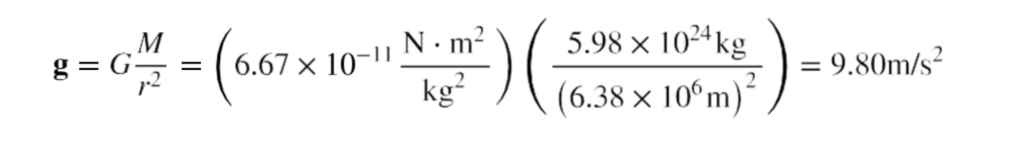
This is a good point to recall the difference between mass and weight. Mass is the amount of matter in an object; weight is the force of attraction between the mass within two objects. Weight can change because g is different on every moon and planet. An object’s mass m does not change but its weight mg can.

We can also derive Kepler’s third law from Newtons’s Universal Law of Gravitation . Applying Newton’s second law of motion to angular motion gives an expression for centripetal force, which can be equated to the expression for force in the universal gravitation equation. This expression can be manipulated to produce the equation for Kepler’s third law. We saw earlier that the expression r3/T2 is a constant for satellites orbiting the same massive object. The derivation of Kepler’s third law from Newton’s law of universal gravitation and Newton’s second law of motion yields that constant:

               r ³ / T² =    GM / 4π²

where M is the mass of the central body about which the satellites orbit (for example, the sun in our solar system).

The universal gravitational constant G is determined experimentally. This definition was first done accurately in 1798 by English scientist Henry Cavendish (1731–1810), more than 100 years after Newton published his universal law of gravitation. The measurement of G is very basic and important because it determines the strength of one of the four forces in nature.

Cavendish’s experiment was very difficult because he measured the tiny gravitational attraction between two ordinary-sized masses (tens of kilograms at most) by using an apparatus like that in the below figure .  Remarkably, his value for G differs by less than 1% from the modern value.

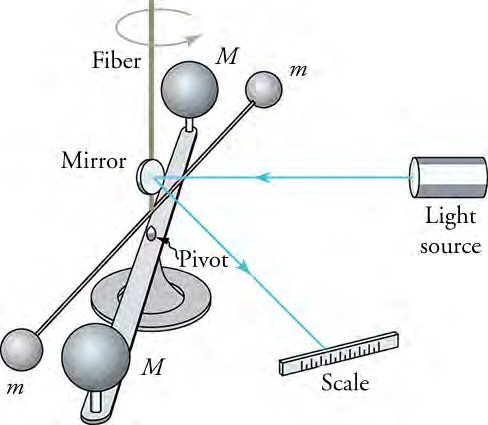
Cavendish used an apparatus like this to measure the gravitational attraction between two suspended spheres (m) and two spheres on a stand (M) by observing the amount of torsion (twisting) created in the fiber. The distance between the masses can be varied to check the dependence of the force on distance. Modern experiments of this type continue to explore gravity

Gravitational Potential Energy

 Gravitational potential energy is the stored energy an object has as a result of its position above Earth’s surface (or another object in space). A roller coaster car at the top of a hill has gravitational potential energy.

Let’s examine how doing work on an object changes the object’s energy. If we apply force to lift a rock off the ground, we increase the rock’s potential energy, PE. If we drop the rock, the force of gravity increases the rock’s kinetic energy as the rock moves downward until it hits the ground.

The force we exert to lift the rock is equal to its weight, w, which is equal to its mass, m, multiplied by acceleration due to gravity, g.

f = w = mg

The work we do on the rock equals the force we exert multiplied by the distance, d, that we lift the rock. The work we do on the rock also equals the rock’s gain in gravitational potential energy, PE_e.

W = PE_e = fmg

Potential energy is particularly useful for forces that change with position, as the gravitational force does over large distances. The change in gravitational potential energy near Earth’s surface is ∆U = mg(y₂ – y₁). This works very well if g does not change significantly between y₁and y₂. We return to the definition of work and potential energy to derive an expression that is correct over larger distances

We know that work (W) is the integral of the dot product between force and distance. Essentially, it is the product of the component of a force along a displacement times that displacement. We define ∆U as the negative of the work done by the force we associate with the potential energy. For clarity, we derive an expression for moving a mass m from distance r₁ from the center of Earth to distance r₂. However, the result can easily be generalized to any two objects changing their separation from one value to another.

Consider the below figure , in which we take m from a distance r₁ from Earth’s center to a distance that is r₂ from the center. Gravity is a conservative force (its magnitude and direction are functions of location only), so we can take any path we wish, and the result for the calculation of work is the same. We take the path shown, as it greatly simplifies the integration. We first move radially outward from distance r₁ to distance r₂ , and then move along the arc of a circle until we reach the final position.

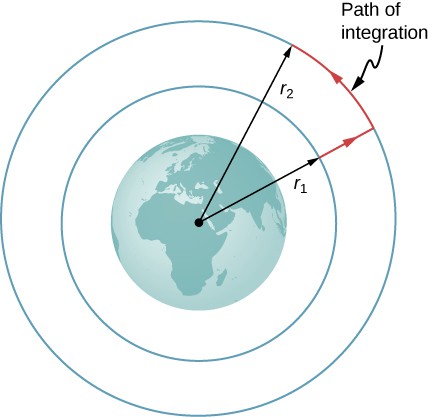
The work integral, which determines the change in potential energy, can be evaluated along the path shown in red.

Note two important items with this definition. First,

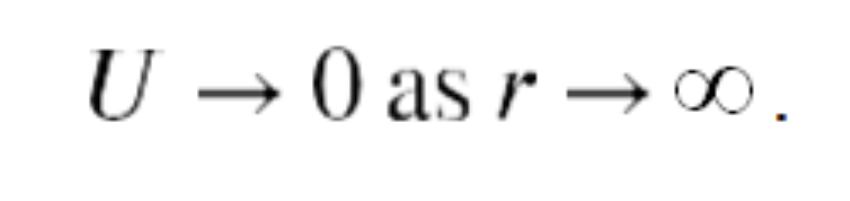
The potential energy is zero when the two masses are infinitely far apart. Only the difference in U is important, so the choice of

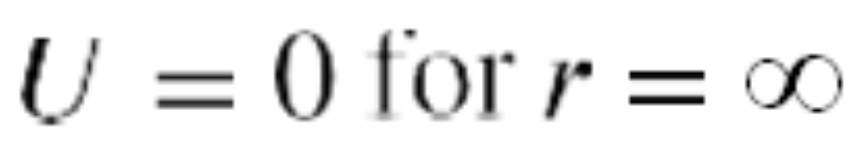
is merely one of convenience. (Recall that in earlier gravity problems, you were free to take U = 0 at the top or bottom of a building, or anywhere.) Second, note that U becomes increasingly more negative as the masses get closer. That is consistent with what you learned about potential energy in Potential Energy and Conservation of Energy. As the two masses are separated, positive work must be done against the force of gravity, and hence, U increases (becomes less negative). All masses naturally fall together under the influence of gravity, falling from a higher to a lower potential energy.

 Escape velocity

Escape velocity is  defined as the minimum initial velocity of an object that is required to escape the surface of a planet (or any large body like a moon) and never return. As usual, we assume no energy lost to an atmosphere, should there be any.

Consider the case where an object is launched from the surface of a planet with an initial velocity directed away from the planet. With the minimum velocity needed to escape, the object would just come to rest infinitely far away, that is, the object gives up the last of its kinetic energy just as it reaches infinity, where the force of gravity becomes zero.

Since U → 0 as r → ∞, this means the total energy is zero. Thus, we find the escape velocity from the surface of an astronomical body of mass M and radius R by setting the total energy equal to zero. At the surface of the body, the object is located at r₁=R  and it has escape velocity V₁= V𝑒𝑠𝑐. It reaches r2=∞ with velocity v₂=0

The escape velocity is the same for all objects, regardless of mass. Also, we are not restricted to the surface of the planet; R can be any starting point beyond the surface of the planet.

In Potential Energy and Conservation of Energy, we described how to apply conservation of energy for systems with conservative forces. We were able to solve many problems, particularly those involving gravity, more simply using conservation of energy. Those principles and problem-solving strategies apply equally well here. The only change is to place the new expression for potential energy into the conservation of energy equation,

E_tot=K₁+U₁=K₂+U₂

Satellite Orbits and Energy

The Moon orbits Earth. In turn, Earth and the other planets orbit the Sun. The space directly above our atmosphere is filled with artificial satellites in orbit. We examine the simplest of these orbits, the circular orbit, to understand the relationship between the speed and period of planets and satellites in relation to their positions and the bodies that they orbit.

Nicolaus Copernicus first suggested that Earth and all other planets orbit the Sun in circles. He further noted that orbital periods increased with distance from the Sun. Later analysis by Kepler showed that these orbits are actually ellipses, but the orbits of most planets in the solar system are nearly circular. Earth’s orbital distance from the Sun varies a mere 2%. The exception is the eccentric orbit of Mercury, whose orbital distance varies nearly 40%.

Determining the orbital speed and orbital period of a satellite is much easier for circular orbits, so we make that assumption in the derivation that follows. As we described in the previous section, an object with negative total energy is gravitationally bound and therefore is in orbit. Our computation for the special case of circular orbits will confirm this. We focus on objects orbiting Earth, but our results can be generalized for other cases.

Consider a satellite of mass m in a circular orbit about Earth at distance r from the center of Earth (as shown in the below figure) . It has centripetal acceleration directed toward the center of Earth. Earth’s gravity is the only force acting, so Newton’s second law gives

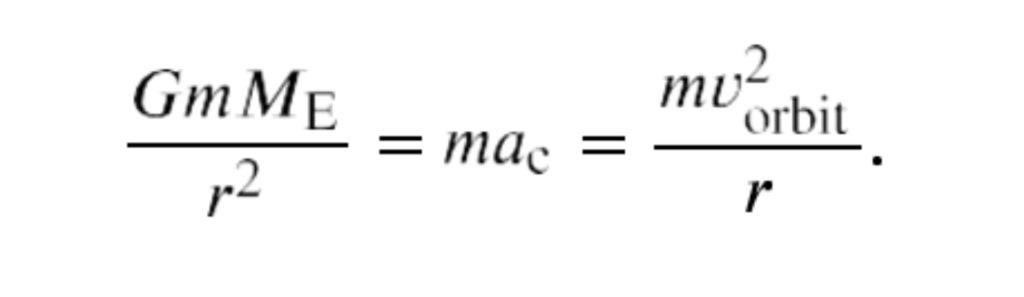
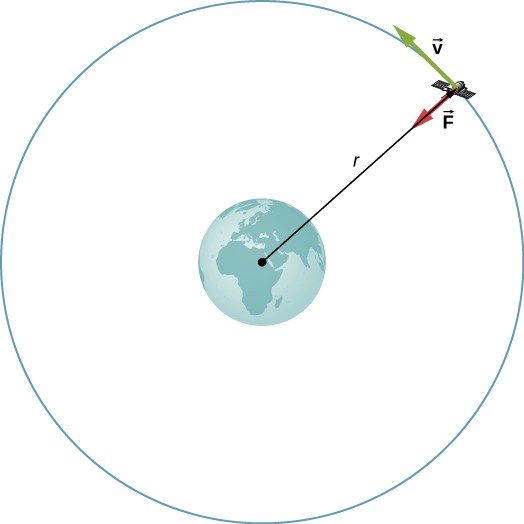
(A satellite of mass m orbiting at radius r from the center of Earth. The gravitational force supplies the centripetal acceleration.)

We solve for the speed of the orbit, noting that m cancels, to get the orbital speed

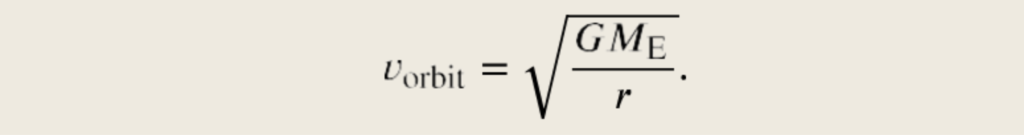
We see in the next section that this represents Kepler’s third law for the case of circular orbits. It also confirms Copernicus’s observation that the period of a planet increases with increasing distance from the Sun.

Astronauts in orbit appear to be weightless, as if they were free-falling towards Earth. In fact, they are in free fall. Consider the trajectories shown in the below figure. (This figure is based on a drawing by Newton in his Principia and also appeared earlier in Motion in Two and Three Dimensions.) All the trajectories shown that hit the surface of Earth have less than orbital velocity. The astronauts would accelerate toward Earth along the noncircular paths shown and feel weightless. (Astronauts actually train for life in orbit by riding in airplanes that free fall for 30 seconds at a time.) But with the correct orbital velocity, Earth’s surface curves away from them at exactly the same rate as they fall toward Earth. Of course, staying the same distance from the surface is the point of a circular orbit

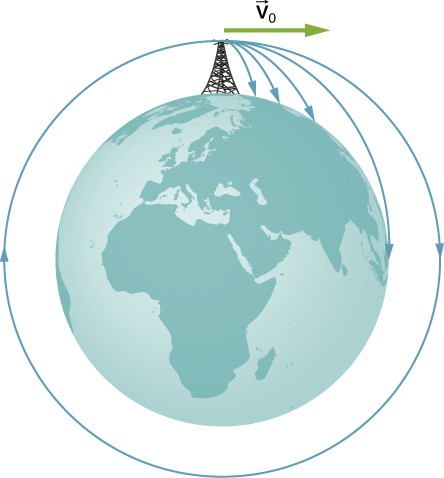
(A circular orbit is the result of choosing a tangential velocity such that Earth’s surface curves away at the same rate as the object falls toward Earth)

Energy in Circular Orbits

In Gravitational Potential Energy and Total Energy, we argued that objects are gravitationally bound if their total energy is negative. The argument was based on the simple case where the velocity was directly away or toward the planet. We now examine the total energy for a circular orbit and show that indeed, the total energy is negative. As we did earlier, we start with Newton’s second law applied to a circular orbit,

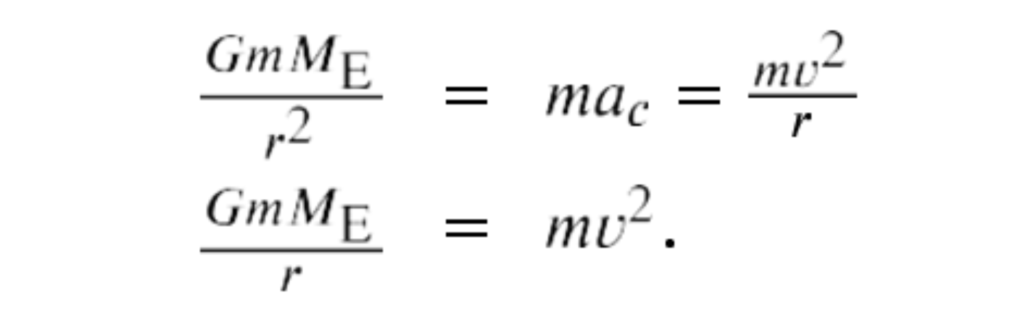
In the last step, we multiplied by r on each side. The right side is just twice the kinetic energy, so we have

K = ½ mv²  = GmM_E / 2r

The total energy is the sum of the kinetic and potential energies, so our final result is

E = K + U

   = GmM_E / 2r  – GmM_E / r

   = – GmM_E / 2r

We can see that the total energy is negative, with the same magnitude as the kinetic energy. For circular orbits, the magnitude of the kinetic energy is exactly one-half the magnitude of the potential energy. Remarkably, this result applies to any two masses in circular orbits about their common center of mass, at a distance r from each other. The proof of this is left as an exercise. We will see in the next section that a very similar expression applies in the case of elliptical orbits

We can see that the total energy is negative, with the same magnitude as the kinetic energy. For circular orbits, the magnitude of the kinetic energy is exactly one-half the magnitude of the potential energy. Remarkably, this result applies to any two masses in circular orbits about their common center of mass, at a distance r from each other. The proof of this is left as an exercise. We will see in the next section that a very similar expression applies in the case of elliptical orbits

“Access for free at openstax.org.”

Take Quiz