Atomic Structure and Symbolism

The development of modern atomic theory revealed much about the inner structure of atoms. It was learned that an atom contains a very small nucleus composed of positively charged protons and uncharged neutrons, surrounded by a much larger volume of space containing negatively charged electrons. The nucleus contains the majority of an atom’s mass because protons and neutrons are much heavier than electrons, whereas electrons occupy almost all of an atom’s volume. The diameter of an atom is on the order of 10−10 m, whereas the diameter of the nucleus is roughly 10−15 m—about 100,000 times smaller. For a perspective about their relative sizes, consider this: If the nucleus were the size of a blueberry, the atom would be about the size of a football stadium

Atoms—and the protons, neutrons, and electrons that compose them—are extremely small. For example, a carbon atom weighs less than 2 X 10^-23 g ,  and an electron has a charge of less than 2 X 10^-19 C (coulomb). When describing the properties of tiny objects such as atoms, we use appropriately small units of measure, such as the atomic mass unit (amu) and the fundamental unit of charge (e). The amu was originally defined based on hydrogen, the lightest element, then later in terms of oxygen. Since 1961, it has been defined with regard to the most abundant isotope of carbon, atoms of which are assigned masses of exactly 12 amu. (This isotope is known as “carbon-12” as will be discussed later in this module.) Thus, one amu is exactly of the mass of one carbon-12 atom ie 1 amu = 1.6605 X 10^-24 g . (The Dalton (Da) and the unified atomic mass unit (u) are alternative units that are equivalent to the amu.) The fundamental unit of charge (also called the elementary charge) equals the magnitude of the charge of an electron (e) with e = 1.602 X 10^-19 Coulomb

A proton has a mass of 1.0073 amu and a charge of 1+. A neutron is a slightly heavier particle with a mass 1.0087 amu and a charge of zero; as its name suggests, it is neutral. The electron has a charge of 1− and is a much lighter particle with a mass of about 0.00055 amu (it would take about 1800 electrons to equal the mass of one proton). The properties of these fundamental particles are summarized in the below table . ( You might notice that the sum of an atom’s subatomic particles does not equal the atom’s actual mass: The total mass of six protons, six neutrons, and six electrons is 12.0993 amu, slightly larger than 12.00 amu. This “missing” mass is known as the mass defect, and you will learn about it in  nuclear chemistry.)

Properties of Subatomic Particles

Name	Location	Charge (C)	Unit Charge	Mass (amu)	Mass (g)
electron	outside nucleus	−1.602 10−19	1−	0.00055	0.00091 10−24
proton	nucleus	1.602 10−19	1+	1.00727	1.67262 10−24
neutron	nucleus	0	0	1.00866	1.67493 10−24

The number of protons in the nucleus of an atom is its atomic number (Z). This is the defining trait of an element: Its value determines the identity of the atom. For example, any atom that contains six protons is the element carbon and has the atomic number 6, regardless of how many neutrons or electrons it may have. A neutral atom must contain the same number of positive and negative charges, so the number of protons equals the number of electrons. Therefore, the atomic number also indicates the number of electrons in an atom. The total number of protons and neutrons in an atom is called its mass number (A). The number of neutrons is therefore the difference between the mass number and the atomic number:

Mass Number (A) = Number of Protons + Number of Neutrons

A – Z = Number of Neutrons

Atoms are electrically neutral if they contain the same number of positively charged protons and negatively charged electrons. When the numbers of these subatomic particles are not equal, the atom is electrically charged and is called an ion. The charge of an atom is defined as follows:

Atomic charge = number of protons − number of electrons

Atoms (and molecules) typically acquire charge by gaining or losing electrons. An atom that gains one or more electrons will exhibit a negative charge and is called an anion. Positively charged atoms called cations are formed when an atom loses one or more electrons. For example, a neutral sodium atom (Z = 11) has 11 electrons. If this atom loses one electron, it will become a cation with a 1+ charge (11 − 10 = 1+). A neutral oxygen atom (Z = 8) has eight electrons, and if it gains two electrons it will become an anion with a 2− charge (8 − 10 = 2−).

Chemical Symbols

A chemical symbol is an abbreviation that we use to indicate an element or an atom of an element. For example, the symbol for mercury is Hg (Figure 2.13). We use the same symbol to indicate one atom of mercury (microscopic domain) or to label a container of many atoms of the element mercury (macroscopic domain).

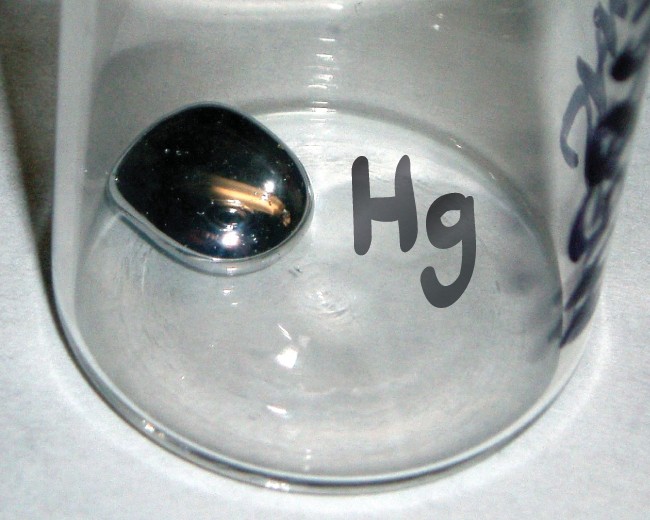
The symbol Hg represents the element mercury regardless of the amount; it could represent one  atom of mercury or a large amount of mercury

The symbols for several common elements and their atoms are listed in the below table . Some symbols are derived from the common name of the element; others are abbreviations of the name in another language. Most symbols have one or two letters, but three-letter symbols have been used to describe some elements that have atomic numbers greater than 112. To avoid confusion with other notations, only the first letter of a symbol is capitalized. For example, Co is the symbol for the element cobalt, but CO is the notation for the compound carbon monoxide, which contains atoms of the elements carbon (C) and oxygen (O). All known elements and their symbols are in the periodic table .

Some Common Elements and Their Symbols

Element	Symbol	Element	Symbol
aluminum	Al	iron	Fe (from ferrum)
bromine	Br	lead	Pb (from plumbum)
calcium	Ca	magnesium	Mg
carbon	C	mercury	Hg (from hydrargyrum)
chlorine	Cl	nitrogen	N
chromium	Cr	oxygen	O
cobalt	Co	potassium	K (from kalium)
copper	Cu (from cuprum)	silicon	Si
fluorine	F	silver	Ag (from argentum)
gold	Au (from aurum)	sodium	Na (from natrium)
helium	He	sulfur	S
hydrogen	H	tin	Sn (from stannum)
iodine	I	zinc	Zn

Traditionally, the discoverer (or discoverers) of a new element names the element. However, until the name is recognized by the International Union of Pure and Applied Chemistry (IUPAC), the recommended name of the new element is based on the Latin word(s) for its atomic number. For example, element 106 was called unnilhexium (Unh), element 107 was called unnilseptium (Uns), and element 108 was called unniloctium (Uno) for several years. These elements are now named after scientists (or occasionally locations); for example, element 106 is now known as seaborgium (Sg) in honor of Glenn Seaborg, a Nobel Prize winner who was active in the discovery of several heavy elements. Element 109 was named in honor of Lise Meitner, who discovered nuclear fission, a phenomenon that would have world-changing impacts; Meitner also contributed to the discovery of some major isotopes, discussed immediately below

Isotopes

The symbol for a specific isotope of any element is written by placing the mass number as a superscript (above the letter) to the left of the element symbol . The atomic number is sometimes written as a subscript (below the letter)  preceding the symbol, but since this number defines the element’s identity, as does its symbol, it is often omitted. For example, magnesium exists as a mixture of three isotopes, each with an atomic number of 12 and with mass numbers of 24, 25, and 26, respectively. These isotopes can be identified as ²⁴Mg, ²⁵Mg, and ²⁶Mg. These isotope symbols are read as “element, mass number” and can be symbolized consistent with this reading. For instance, ²⁴Mg is read as “magnesium 24,” and can be written as “magnesium-24” or “Mg-24.” ²⁵Mg is read as “magnesium 25,” and can be written as “magnesium-25” or “Mg-25.” All magnesium atoms have 12 protons in their nucleus. They differ only because a 24Mg atom has 12 neutrons in its nucleus, a ²⁵Mg atom has 13 neutrons, and a ²⁶Mg has 14 neutrons

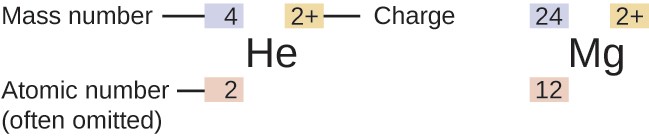
The symbol for an atom indicates the element via its usual two-letter symbol, the mass number as a left superscript, the atomic number as a left subscript (sometimes omitted), and the charge as a right superscript

Information about the naturally occurring isotopes of elements with atomic numbers 1 through 10 is given in the below table . Note that in addition to standard names and symbols, the isotopes of hydrogen are often referred to using common names and accompanying symbols. Hydrogen-2, symbolized ²H, is also called deuterium and sometimes symbolized D. Hydrogen-3, symbolized ³H, is also called tritium and sometimes symbolized T

Nuclear Compositions of Atoms of the Very Light Elements

Element	Symbol	Atomic Number	Number of Protons	Number of Neutrons	Mass (amu)	% Natural Abundance
hydrogen	(protium)	1	1	0	1.0078	99.989
	(deuterium)	1	1	1	2.0141	0.0115
	(tritium)	1	1	2	3.01605	— (trace)
helium		2	2	1	3.01603	0.00013
		2	2	2	4.0026	100
lithium		3	3	3	6.0151	7.59
		3	3	4	7.0160	92.41
beryllium		4	4	5	9.0122	100
boron		5	5	5	10.0129	19.9
		5	5	6	11.0093	80.1
carbon		6	6	6	12.0000	98.89
		6	6	7	13.0034	1.11
		6	6	8	14.0032	— (trace)
nitrogen		7	7	7	14.0031	99.63
		7	7	8	15.0001	0.37
oxygen		8	8	8	15.9949	99.757
		8	8	9	16.9991	0.038
		8	8	10	17.9992	0.205
fluorine		9	9	10	18.9984	100
neon		10	10	10	19.9924	90.48

Atomic Mass

Because each proton and each neutron contribute approximately one amu to the mass of an atom, and each electron contributes far less, the atomic mass of a single atom is approximately equal to its mass number (a whole number). However, the average masses of atoms of most elements are not whole numbers because most elements exist naturally as mixtures of two or more isotopes.

The mass of an element shown in a periodic table or listed in a table of atomic masses is a weighted, average mass of all the isotopes present in a naturally occurring sample of that element. This is equal to the sum of each individual isotope’s mass multiplied by its fractional abundance

For example, the element boron is composed of two isotopes: About 19.9% of all boron atoms are ¹⁰B with a mass of 10.0129 amu, and the remaining 80.1% are ¹¹B with a mass of 11.0093 amu. The average atomic mass for boron is calculated to be:

Boron Average Mass =  (0.199 X 10.0129 amu) + (0.801 X 11.0093 amu)
= 11.99 amu + 8.82 amu
= 10.81 amu

It is important to understand that no single boron atom weighs exactly 10.8 amu; 10.8 amu is the average mass of all boron atoms, and individual boron atoms weigh either approximately 10 amu or 11 amu.

Chemical Formulas

A molecular formula is a representation of a molecule that uses chemical symbols to indicate the types of atoms followed by subscripts to show the number of atoms of each type in the molecule. (A subscript is used only when more than one atom of a given type is present.) Molecular formulas are also used as abbreviations for the names of compounds

The structural formula for a compound gives the same information as its molecular formula (the types and numbers of atoms in the molecule) but also shows how the atoms are connected in the molecule. The structural formula for methane contains symbols for one C atom and four H atoms, indicating the number of atoms in the molecule  (Below figure) . The lines represent bonds that hold the atoms together. (A chemical bond  is an attraction between atoms or ions that holds them together in a molecule or a crystal.  For now, simply know that the lines are an indication of how the atoms are connected in a molecule. A ball-and-stick model shows the geometric arrangement of the atoms with atomic sizes not to scale, and a space-filling model shows the relative sizes of the atoms

A methane molecule can be represented as (a) a molecular formula, (b) a structural formula, (c) a ball-and-stick model, and (d) a space-filling model. Carbon and hydrogen atoms are represented by black and white spheres, respectively

Although many elements consist of discrete, individual atoms, some exist as molecules made up of two or more atoms of the element chemically bonded together. For example, most samples of the elements hydrogen, oxygen, and nitrogen are composed of molecules that contain two atoms each (called diatomic molecules) and thus have the molecular formulas H₂, O₂, and N₂, respectively. Other elements commonly found as diatomic molecules are fluorine (F₂), chlorine (Cl₂), bromine (Br₂), and iodine (I₂). The most common form of the element sulfur is composed of molecules that consist of eight atoms of sulfur; its molecular formula is S₈

A molecule of sulfur is composed of eight sulfur atoms and is therefore written as S₈. It can be represented as (a) a structural formula, (b) a ball-and-stick model, and (c) a space-filling model. Sulfur atoms are represented by yellow spheres

It is important to note that a subscript following a symbol and a number in front of a symbol do not represent the same thing; for example, H₂ and 2H represent distinctly different species. H₂ is a molecular formula; it represents a diatomic molecule of hydrogen, consisting of two atoms of the element that are chemically bonded together. The expression 2H, on the other hand, indicates two separate hydrogen atoms that are not combined as a unit. The expression 2H₂ represents two molecules of diatomic hydrogen

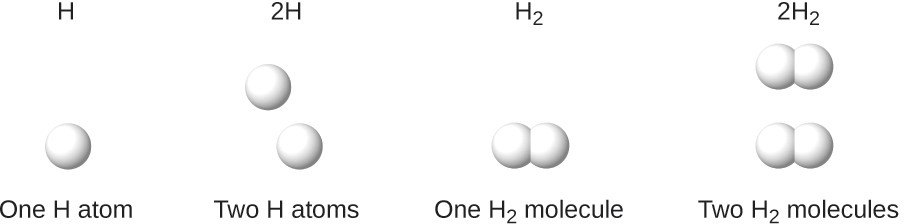
The symbols H, 2H, H₂, and 2H₂ represent very different entities

Compounds are formed when two or more elements chemically combine, resulting in the formation of bonds. For example, hydrogen and oxygen can react to form water, and sodium and chlorine can react to form table salt. We sometimes describe the composition of these compounds with an empirical formula, which indicates the types of atoms present and the simplest whole-number ratio of the number of atoms (or ions) in the compound. For example, titanium dioxide (used as pigment in white paint and in the thick, white, blocking type of sunscreen) has an empirical formula of TiO₂. This identifies the elements titanium (Ti) and oxygen (O) as the constituents of titanium dioxide, and indicates the presence of twice as many atoms of the element oxygen as atoms of the element titanium

The white compound titanium dioxide provides effective protection from the sun. (b) A crystal of titanium dioxide, TiO₂, contains titanium and oxygen in a ratio of 1 to 2. The titanium atoms are gray and the oxygen atoms are red. (credit a: modification of work by “osseous”/Flickr)

As discussed previously, we can describe a compound with a molecular formula, in which the subscripts indicate the actual numbers of atoms of each element in a molecule of the compound. In many cases, the molecular formula of a substance is derived from experimental determination of both its empirical formula and its molecular mass (the sum of atomic masses for all atoms composing the molecule). For example, it can be determined experimentally that benzene contains two elements, carbon (C) and hydrogen (H), and that for every carbon atom in benzene, there is one hydrogen atom. Thus, the empirical formula is CH. An experimental determination of the molecular mass reveals that a molecule of benzene contains six carbon atoms and six hydrogen atoms, so the molecular formula for benzene is C₆H₆

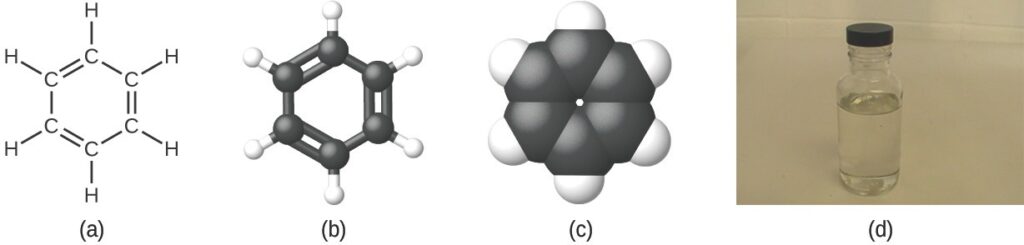
Benzene, C₆H₆, is produced during oil refining and has many industrial uses. A benzene molecule can be represented as (a) a structural formula, (b) a ball-and-stick model, and (c) a space-filling model. (d) Benzene is a clear liquid. (credit d: modification of work by Sahar Atwa)

For example, the molecular formula for acetic acid, the component that gives vinegar its sharp taste, is C₂H₄O₂. This formula indicates that a molecule of acetic acid  (Below Figure) contains two carbon atoms, four hydrogen atoms, and two oxygen atoms. The ratio of atoms is 2:4:2. Dividing by the lowest common denominator (2) gives the simplest, whole-number ratio of atoms, 1:2:1, so the empirical formula is CH₂O. Note that a molecular formula is always a whole- number multiple of an empirical formula.

• Vinegar contains acetic acid, C₂H₄O₂, which has an empirical formula of CH₂O. It can be represented as (b) a structural formula and (c) as a ball-and-stick model. (credit a: modification of work by “HomeSpot HQ”/Flickr)

It is important to be aware that it may be possible for the same atoms to be arranged in different ways: Compounds with the same molecular formula may have different atom-to-atom bonding and therefore different structures. For example, could there be another compound with the same formula as acetic acid, C₂H₄O₂? And if so, what would be the structure of its molecules?

Two C atoms, four H atoms, and two O atoms can also be arranged to form a methyl formate, which is used in manufacturing, as an insecticide, and for quick-drying finishes. Methyl formate molecules have one of the oxygen atoms between the two carbon atoms, differing from the arrangement in acetic acid molecules. Acetic acid and methyl formate are examples of isomers—compounds with the same chemical formula but different molecular structures (Below Figure) . Note that this small difference in the arrangement of the atoms has a major effect on their respective chemical properties. You would certainly not want to use a solution of methyl formate as a substitute for a solution of acetic acid (vinegar) when you make salad dressing.

Molecules of (a) acetic acid and methyl formate (b) are structural isomers; they have the same formula (C₂H₄O₂) but different structures (and therefore different chemical properties).

Formula Mass and the Mole Concept

Many argue that modern chemical science began when scientists started exploring the quantitative as well as the qualitative aspects of chemistry. For example, Dalton’s atomic theory was an attempt to explain the results of measurements that allowed him to calculate the relative masses of elements combined in various compounds. Understanding the relationship between the masses of atoms and the chemical formulas of compounds allows us to quantitatively describe the composition of substances.

Formula Mass

We have seen the development of the atomic mass unit, the concept of average atomic masses, and the use of chemical formulas to represent the elemental makeup of substances. These ideas can be extended to calculate the formula mass of a substance by summing the average atomic masses of  all the atoms represented in the substance’s formula.

Formula Mass for Covalent Substances

For covalent substances, the formula represents the numbers and types of atoms composing a single molecule of the substance; therefore, the formula mass may be correctly referred to as a molecular mass. Consider chloroform (CHCl₃), a covalent compound once used as a surgical anesthetic and now primarily used in the production of tetrafluoroethylene, the building block for the “anti-stick” polymer, Teflon. The molecular formula of chloroform indicates that a single molecule contains one carbon atom, one hydrogen atom, and three chlorine atoms. The average molecular mass of a chloroform molecule is therefore equal to the sum of the average atomic masses of these atoms. Below figure outlines the calculations used to derive the molecular mass of chloroform, which is 119.37 amu

The average mass of a chloroform molecule, CHCl₃, is 119.37 amu, which is the sum of the average atomic masses of each of its constituent atoms. The model shows the molecular structure of chloroform

Likewise, the molecular mass of an aspirin molecule, C₉H₈O₄, is the sum of the atomic masses of nine carbon atoms, eight hydrogen atoms, and four oxygen atoms, which amounts to 180.15 amu

The average mass of an aspirin molecule is 180.15 amu. The model shows the molecular structure of aspirin, C₉H₈O₄

Formula Mass for Ionic Compounds

Ionic compounds are composed of discrete cations and anions combined in ratios to yield electrically neutral bulk matter. The formula mass for an ionic compound is calculated in the same way as the formula mass for covalent compounds: by summing the average atomic masses of all the atoms in the compound’s formula. Keep in mind, however, that the formula for an ionic compound does not represent the composition of a  discrete molecule, so it may not correctly be referred to as the “molecular mass.”

As an example, consider sodium chloride, NaCl, the chemical name for common table salt. Sodium chloride is an ionic compound composed of sodium cations, Na+, and chloride anions, Cl−, combined in a 1:1 ratio. The formula mass for this compound is computed as 58.44 amu

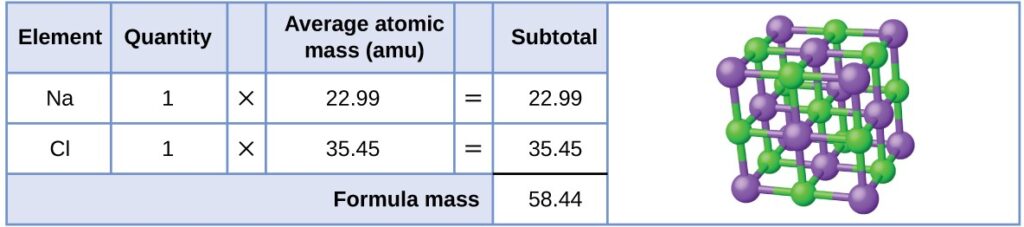
Table salt, NaCl, contains an array of sodium and chloride ions combined in a 1:1 ratio. Its formula mass is 58.44 amu

Note that the average masses of neutral sodium and chlorine atoms were used in this computation, rather than   the masses for sodium cations and chlorine anions. This approach is perfectly acceptable when computing the formula mass of an ionic compound. Even though a sodium cation has a slightly smaller mass than a sodium atom (since it is missing an electron), this difference will be offset by the fact that a chloride anion is slightly more massive than a chloride atom (due to the extra electron). Moreover, the mass of an electron is negligibly small with respect to the mass of a typical atom. Even when calculating the mass of an isolated ion, the missing or additional electrons can generally be ignored, since their contribution to the overall mass is negligible, reflected only in the nonsignificant digits that will be lost when the computed mass is properly rounded. The few exceptions to this guideline are very light ions derived from elements with precisely known atomic masses.

The Mole Concept and Molar Mass

The identity of a substance is defined not only by the types of atoms or ions it contains, but by the quantity of each type of atom or ion. For example, water, H₂O, and hydrogen peroxide, H₂O₂, are alike in that their respective molecules are composed of hydrogen and oxygen atoms. However, because a hydrogen peroxide molecule contains two oxygen atoms, as opposed to the water molecule, which has only one, the two substances exhibit very different properties. Today, sophisticated instruments allow the direct measurement of these defining microscopic traits; however, the same traits were originally derived from the measurement of macroscopic properties (the masses and volumes of bulk quantities of matter) using relatively simple tools (balances and volumetric glassware). This experimental approach required the introduction of a new unit for amount of substances, the mole, which remains indispensable in modern chemical science.

The mole is an amount unit similar to familiar units like pair, dozen, gross, etc. It provides a specific measure of the number of atoms or molecules in a sample of matter. One Latin connotation for the word “mole” is “large mass” or “bulk,” which is consistent with its use as the name for this unit. The mole provides a link between an easily measured macroscopic property, bulk mass, and an  extremely  important  fundamental  property, number of atoms, molecules, and so forth. A mole of substance is that amount in which there are 6.02214076 X 10²³ discrete entities (atoms or molecules). This large number is a fundamental constant known as Avogadro’s number (N_A) or the Avogadro constant in honor of Italian scientist Amedeo Avogadro. This constant is properly reported with an explicit unit of “per mole,” a conveniently rounded version being 6.022 X 10²³ / mol

Consistent with its definition as an amount unit, 1 mole of any element contains the same number of atoms as 1 mole of any other element. The masses of 1 mole of different elements, however, are different, since the masses of the individual atoms are drastically different. The molar mass of an element (or compound) is the mass in grams of 1 mole of that substance, a property expressed in units of grams per mole (g/mol)

Each sample contains 6.022 X 10 ²³  atoms —1.00 mol of atoms. From left to right (top row): 65.4 g zinc, 12.0 g carbon, 24.3 g magnesium, and 63.5 g copper. From left to right (bottom row): 32.1 g sulfur, 28.1 g silicon, 207 g lead, and 118.7 g tin. (credit: modification of work by Mark Ott)

The molar mass of any substance is numerically equivalent to its atomic or formula weight in amu. Per the amu definition, a single 12C atom weighs 12 amu (its atomic mass is 12 amu). A mole of 12C weighs 12 g (its molar mass is 12 g/mol). This relationship holds for all elements, since their atomic masses are measured relative to that of the amu-reference substance, 12C. Extending this principle, the molar mass of a compound in   grams is likewise numerically equivalent to its formula mass in amu

Each sample contains 6.02 X 10²³  molecules or formula units—1.00 mol of the compound or element. Clock-wise from the upper left: 130.2 g of C₈H₁₇OH (1-octanol, formula mass 130.2 amu), 454.4 g of HgI₂ (mercury(II) iodide, formula mass 454.4 amu), 32.0 g of CH₃OH (methanol, formula mass 32.0 amu) and 256.5 g of S₈ (sulfur, formula mass 256.5 amu). (credit: Sahar Atwa)

While atomic mass and molar mass are numerically equivalent, keep in mind that they are vastly different in terms of scale, as represented by the vast difference in the magnitudes of their respective units (amu versus g). To appreciate the enormity of the mole, consider a small drop of water weighing about 0.03 g . Although this represents just a tiny fraction of 1 mole of water (~18 g), it contains more water molecules than can be clearly imagined. If the molecules were distributed equally among the roughly seven billion people on earth, each person would receive more than 100 billion molecules.

Determining Empirical and Molecular Formulas

The previous section discussed the relationship between the bulk mass of a substance and the number of atoms or molecules it contains (moles). Given the chemical formula of the substance, one may determine the amount of the substance (moles) from its mass, and vice versa. But what if the chemical formula of a substance is unknown? In this section, these same principles will be applied to derive the chemical formulas of unknown substances from experimental mass measurements

Percent Composition

The elemental makeup of a compound defines its chemical identity, and chemical formulas are the most succinct way of representing this elemental makeup. When a compound’s formula is unknown, measuring the mass of each of its constituent elements is often the first step in the process of determining the formula experimentally. The results of these measurements permit the calculation of the compound’s percent composition, defined as the percentage by mass of each element in the compound.

For example, consider a gaseous compound composed solely of carbon and hydrogen. The percent composition of this compound could be represented as follows :

% H = ( Mass H / Mass Compound ) X 100%

% C = ( Mass C / Mass Compound ) X 100%

If analysis of a 10.0-g sample of this gas showed it to contain 2.5 g H and 7.5 g C, the percent composition would be calculated to be 25% H and 75% C:

% H = (0.25 g / 10 g ) X 100% = 25%

% C = (0.75 g / 10 g ) X 100% = 75%

Determining Percent Composition from Molecular or Empirical Formulas

Percent composition is also useful for evaluating the relative abundance of a given element in different compounds of known formulas. As one example, consider the common nitrogen-containing fertilizers ammonia (NH₃), ammonium nitrate (NH₄NO₃), and urea (CH₄N₂O). The element nitrogen is the active ingredient for agricultural purposes, so the mass percentage of nitrogen in the compound is a practical and economic concern for consumers choosing among these fertilizers. For these sorts of applications, the percent composition of a compound is easily derived from its formula mass and the atomic masses of its constituent elements. A molecule of NH₃ contains one N atom weighing 14.01 amu and three H atoms weighing a total of ( 3 X 1.008 amu) = 3.024 amu . The formula mass of ammonia is therefore (14.01 amu + 3.024 amu) = 17.03 amu, and its percent composition is:

% N = (14.01  / 17.03) X 100 = 82.2%

% H = (3.024 / 17.03) X 100 = 18.8 %

This same approach may be taken considering a pair of molecules, a dozen molecules, or a mole of molecules, etc. The latter amount is most convenient and would simply involve the use of molar masses instead of atomic and formula masses. As long as the molecular or empirical formula of the compound in question is known, the percent composition may be derived from the atomic or molar masses of the compound’s elements

Determination of Empirical Formulas :

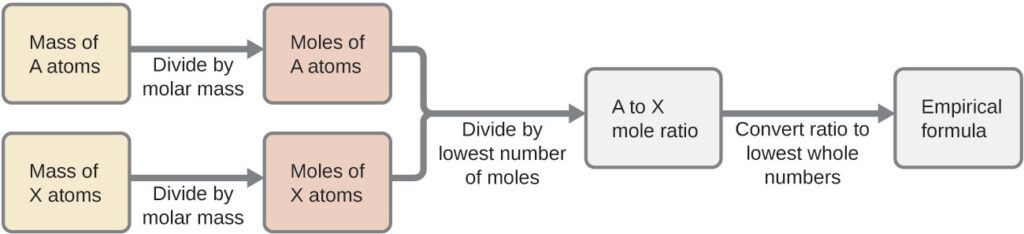
The most common approach to determining a compound’s chemical formula is to first measure the masses of its constituent elements. However, keep in mind that chemical formulas represent the relative numbers, not masses, of atoms in the substance. Therefore, any experimentally derived data involving mass must be used to derive the corresponding numbers of atoms in the compound. This is accomplished using molar masses to convert the mass of each element to a number of moles. These molar amounts are used to compute whole-number ratios that can be used to derive the empirical formula of the substance

In summary, empirical formulas are derived from experimentally measured element masses by:

1. Deriving the number of moles of each element from its mass
2. Dividing each element’s molar amount by the smallest molar amount to yield subscripts for a tentative empirical formula
3. Multiplying all coefficients by an integer, if necessary, to ensure that the smallest whole-number ratio of subscripts is obtained

Below Figure outlines this procedure in flow chart fashion for a substance containing elements A and X.

Finally, with regard to deriving empirical formulas, consider instances in which a compound’s percent composition is available rather than the absolute masses of the compound’s constituent elements. In such cases, the percent composition can be used to calculate the masses of elements present in any convenient mass of compound; these masses can then be used to derive the empirical formula in the usual fashion.

Derivation of Molecular Formulas

Recall that empirical formulas are symbols representing the relative numbers of a compound’s elements. Determining the absolute numbers of atoms that compose a single molecule of a covalent compound requires knowledge of both its empirical formula and its molecular mass or molar mass. These quantities may be determined experimentally by various measurement techniques. Molecular mass, for example, is often derived from the mass spectrum of the compound  . Molar mass can be measured by a number of experimental methods

Molecular formulas are derived by comparing the compound’s molecular or molar mass to its empirical formula mass. As the name suggests, an empirical formula mass is the sum of the average atomic masses of all the atoms represented in an empirical formula. If the molecular (or molar) mass of the substance is known, it may be divided by the empirical formula mass to yield the number of empirical formula units per molecule (n)

Molarity

Mixtures—samples of matter containing two or more substances physically combined—are more commonly encountered in nature than are pure substances.

Similar to a pure substance, the relative composition of a mixture plays an important role in determining its properties. The relative amount of oxygen in a planet’s atmosphere determines its ability to sustain aerobic life. The relative amounts of iron, carbon, nickel, and other elements in steel (a mixture known as an “alloy”) determine its physical strength and resistance to corrosion. The relative amount of the active ingredient in a medicine determines its effectiveness in achieving the desired pharmacological effect. The relative amount of sugar in a beverage determines its sweetness . This section will describe one of the most common ways in which the relative compositions of mixtures may be quantified.

Sugar is one of many components in the complex mixture known as coffee. The amount of sugar in a given amount of coffee is an important determinant of the beverage’s sweetness. (credit: Jane Whitney)

Solutions

Solutions have previously been defined as homogeneous mixtures, meaning that the composition of the mixture (and therefore its properties) is uniform throughout its entire volume. Solutions occur frequently in nature and have also been implemented in many forms of manmade technology. A more thorough treatment of solution properties is provided in the chapter on solutions and colloids, but provided here is an introduction to some of the basic properties of solutions.

The relative amount of a given solution component is known as its concentration. Often, though not always, a solution contains one component with a concentration that is significantly greater than that of all other components. This component is called the solvent and may be viewed as the medium in which the other components are dispersed, or dissolved. Solutions in which water is the solvent are, of course, very common on our planet. A solution in which water is the solvent is called an aqueous solution.

A solute is a component of a solution that is typically present at a much lower concentration than the solvent. Solute concentrations are often described with qualitative terms such as dilute (of relatively low concentration) and concentrated (of relatively high concentration).

Concentrations may be quantitatively assessed using a wide variety of measurement units, each convenient for particular applications. Molarity (M) is a useful concentration unit for many applications in chemistry.

Molarity is defined as the number of moles of solute in exactly 1 liter (1 L) of the solution:

ie  [ M = ( mol Solute / L solution) ]

Mass Percentage

Percentages are also commonly used to express the composition of mixtures, including solutions. The mass percentage of a solution component is defined as the ratio of the component’s mass to the solution’s mass, expressed as a percentage

Mass Percentage = (Mass of Component / Mass of Solution) X 100 %

Mass percentage is also referred to by similar names such as percent mass, percent weight, weight/weight percent, and other variations on this theme. The most common symbol for mass percentage is simply the percent sign, %, although more detailed symbols are often used including %mass, %weight, and (w/w)%. Use of these more detailed symbols can prevent confusion of mass percentages with other types of percentages, such as volume percentages .

Mass percentages are popular concentration units for consumer products. The label of a typical liquid bleach bottle cites the concentration of its active ingredient, sodium hypochlorite (NaOCl), as being 7.4%. A 100.0-g sample of bleach would therefore contain 7.4 g of NaOCl

Liquid bleach is an aqueous solution of sodium hypochlorite (NaOCl). This brand has a concentration of 7.4% NaOCl by mass

Volume Percentage

Liquid volumes over a wide range of magnitudes are conveniently measured using common and relatively inexpensive laboratory equipment. The concentration of a solution formed by dissolving a liquid solute in a liquid solvent is therefore often expressed as a volume percentage, %vol or (v/v)%

Volume Percentage = (Volume Solute / Volume Solution) X 100 %

Mass-Volume Percentage

“Mixed” percentage units, derived from the mass of solute and the volume of solution, are popular for certain biochemical and medical applications. A mass-volume percent is a ratio of a solute’s mass to the solution’s volume expressed as a percentage. The specific units used for solute mass and solution volume may vary, depending on the solution. For example, physiological saline solution, used to prepare intravenous fluids, has a concentration of 0.9% mass/volume (m/v), indicating that the composition is 0.9 g of solute per 100 mL of solution. The concentration of glucose in blood (commonly referred to as “blood sugar”) is also typically expressed in terms of a mass-volume ratio. Though not expressed explicitly as a percentage, its concentration is usually given in milligrams of glucose per deciliter (100 mL) of blood

“Mixed” mass-volume units are commonly encountered in medical settings. (a) The NaCl concentration of physiological saline is 0.9% (m/v). (b) This device measures glucose levels in a sample of blood. The normal range for glucose concentration in blood (fasting) is around 70–100 mg/dL. (credit a: modification of work by “The National Guard”/Flickr; credit b: modification of work by Biswarup Ganguly)

Parts per Million and Parts per Billion

Very low solute concentrations are often expressed using appropriately small units such as parts per million (ppm) or parts per billion (ppb). Like percentage (“part per hundred”) units, ppm and ppb may be defined in terms of masses, volumes, or mixed mass-volume units. There are also ppm and ppb units defined with respect to numbers of atoms and molecules

Both ppm and ppb are convenient units for reporting the concentrations of pollutants and other trace contaminants in water. Concentrations of these contaminants are typically very low in treated and natural waters, and their levels cannot exceed relatively low concentration thresholds without causing adverse effects on health and wildlife. For example, the EPA has identified the maximum safe level of fluoride ion in tap water to be 4 ppm. Inline water filters are designed to reduce the concentration of fluoride and several other trace- level contaminants in tap water

• In some areas, trace-level concentrations of contaminants can render unfiltered tap water unsafe for drinking and cooking. (b) Inline water filters reduce the concentration of solutes in tap water. (credit a: modification of work by Jenn Durfey; credit b: modification of work by “vastateparkstaff”/Wikimedia commons)

Stoichiometry of Chemical Reactions

The description of  how to symbolize chemical reactions using chemical equations, how   to classify some common chemical reactions by identifying patterns of reactivity, and how to determine the quantitative relations between the amounts of substances involved in chemical reaction is called  the reaction stoichiometry.

Writing and Balancing Chemical Equations

When atoms gain or lose electrons to yield ions, or combine with other atoms to form molecules, their symbols are modified or combined to generate chemical formulas that appropriately represent these species. Extending this symbolism to represent both the identities and the relative quantities of substances undergoing a chemical (or physical) change involves writing and balancing a chemical equation.

Consider as an example the reaction between one methane molecule (CH₄) and two diatomic oxygen molecules (O₂) to produce one carbon dioxide molecule (CO₂) and two water molecules (H₂O). The chemical equation representing this process is provided in the upper half of the below figure, with space-filling molecular models shown in the lower half of the figure.

The reaction between methane and oxygen to yield carbon dioxide and water (shown at bottom) may be represented by a chemical equation using formulas (top).

This example illustrates the fundamental aspects of any chemical equation:

1. The substances undergoing reaction are called reactants, and their formulas are placed on the left side of the equation.
2. The substances generated by the reaction are called products, and their formulas are placed on the right side of the equation.
3. Plus signs (+) separate individual reactant and product formulas, and an arrow -> separates the reactant and product (left and right) sides of the equation.
4. The relative numbers of reactant and product species are represented by coefficients (numbers placed immediately to the left of each formula). A coefficient of 1 is typically omitted.

It is common practice to use the smallest possible whole-number coefficients in a chemical equation, as is done in this example. Realize, however, that these coefficients represent the relative numbers of reactants and products, and, therefore, they may be correctly interpreted as ratios. Methane and oxygen react to yield carbon dioxide and water in a 1:2:1:2 ratio. This ratio is satisfied if the numbers of these molecules are, respectively, 1-2-1-2 , or 2-4-2-4, or 3-6-3-6, and so on . Likewise, these coefficients may be interpreted with regard to any amount (number) unit, and so this equation may be correctly read in many ways, including:

• One methane molecule and two oxygen molecules react to yield one carbon dioxide molecule and two water molecules.
• One dozen methane molecules and two dozen oxygen molecules react to yield one dozen carbon dioxide molecules and two dozen water molecules.
• One mole of methane molecules and 2 moles of oxygen molecules react to yield 1 mole of carbon dioxide molecules and 2 moles of water molecules

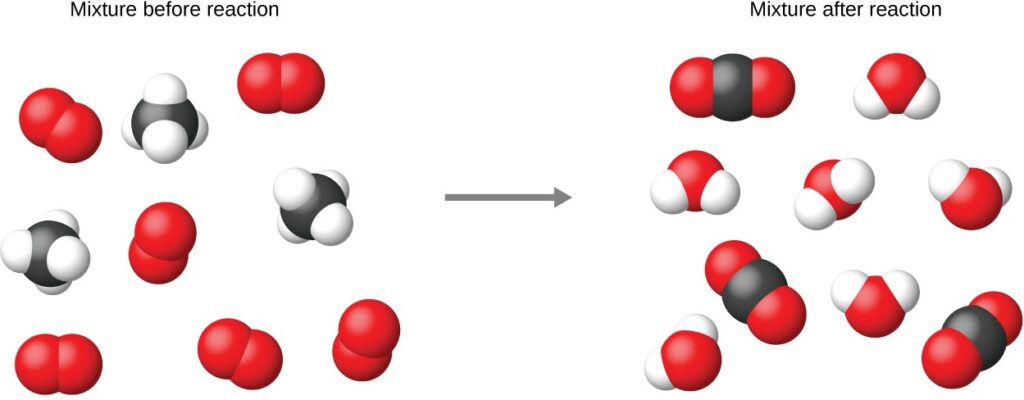
Regardless of the absolute numbers of molecules involved, the ratios between numbers of molecules of each species that react (the reactants) and molecules of each species that form (the products) are the same and are given by the chemical reaction equation

Balancing Equations

A chemical equation is balanced, if  equal numbers of atoms for each element involved in the reaction are represented on the reactant and product sides. This is a requirement the equation must satisfy to be consistent with the law of conservation of matter. It may be confirmed by simply summing the numbers of atoms on either side of the arrow and comparing these sums to ensure they are equal. Note that the number of atoms for a given element is calculated by multiplying the coefficient of any formula containing that element by the element’s subscript in the formula. If an element appears in more than one formula on a given side of the equation, the number of atoms represented in each must be computed and then added together

A balanced chemical equation provides a great deal of information in a very succinct format. Chemical formulas provide the identities of the reactants and products involved in the chemical change, allowing classification of the reaction. Coefficients provide the relative numbers of these chemical species, allowing a quantitative assessment of the relationships between the amounts of substances consumed and produced by the reaction. These quantitative relationships are known as the reaction’s stoichiometry, a term derived from the Greek words stoicheion (meaning “element”) and metron (meaning “measure”). In this module, the use of balanced chemical equations for various stoichiometric applications is explored

The general approach to using stoichiometric relationships is similar in concept to the way people go about many common activities. Food preparation, for example, offers an appropriate comparison. A recipe for making eight pancakes calls for 1 cup pancake mix, ¾ cup milk , and one egg. The “equation” representing the  preparation of pancakes per this recipe is

1 cup pancake mix + ¾ cup milk + 1 egg ——> 8 pancakes

If two dozen pancakes are needed for a big family breakfast, the ingredient amounts must be increased proportionally according to the amounts given in the recipe. For example, the number of eggs required to make 24 pancakes is

24 pancakes X ( 1 egg / 8 pancakes) = 3 eggs

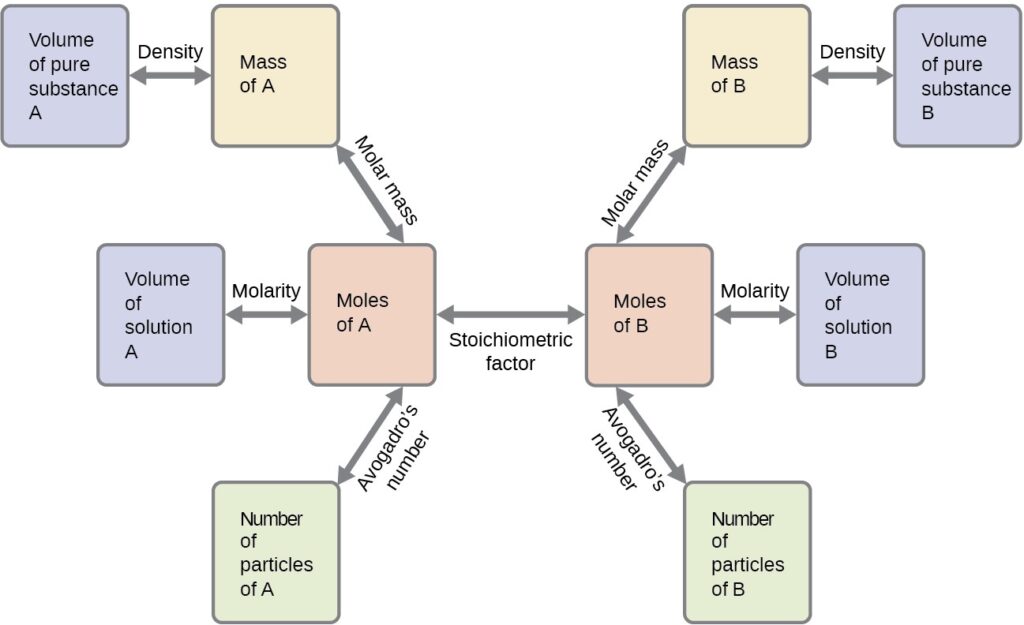
Balanced chemical equations are used in much the same fashion to determine the amount of one reactant required to react with a given amount of another reactant, or to yield a given amount of product, and so forth. The coefficients in the balanced equation are used to derive stoichiometric factors that permit computation of the desired quantity

Numerous variations on the beginning and ending computational steps are possible depending upon what particular quantities are provided and sought (volumes, solution concentrations, and so forth). Regardless of the details, all these calculations share a common essential component: the use of stoichiometric factors derived from balanced chemical equations. Below Figure  provides a general outline of the various computational steps associated with many reaction stoichiometry calculations.

Reaction Yields

The relative amounts of reactants and products represented in a balanced chemical equation are often referred to as stoichiometric amounts. All the exercises of the preceding module involved stoichiometric amounts of reactants. For example, when calculating the amount of product generated from a given amount of reactant, it was assumed that any other reactants required were available in stoichiometric amounts (or greater).

Limiting Reactant

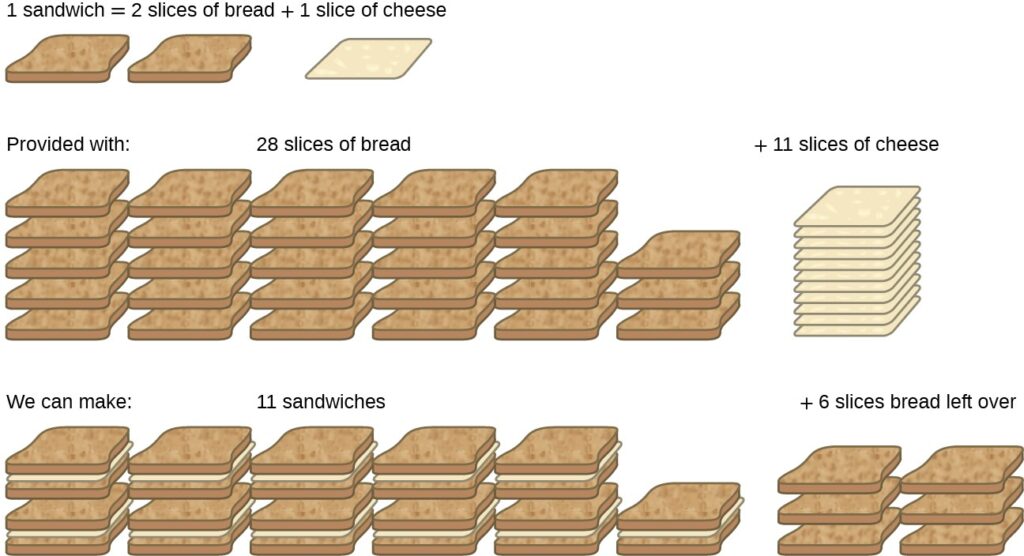
Consider another food analogy, making grilled cheese sandwiches

1 slice of cheese + 2 slices of Bread ———->1 sandwich

Stoichiometric amounts of sandwich ingredients for this recipe are bread and cheese slices in a 2:1 ratio

If you are Provided with 28 slices of bread and 11 slices of cheese, you may prepare 11 sandwiches per the provided recipe, using all the provided cheese and having six slices of bread left over. In this scenario, the number of sandwiches prepared has been limited by the number of cheese slices, and the bread slices have been provided in excess.

Consider this concept now with regard to a chemical process, the reaction of hydrogen with chlorine to yield  hydrogen chloride

H₂​+Cl₂ →2HCl

The balanced equation shows the hydrogen and chlorine react in a 1:1 stoichiometric ratio. If these reactants are provided in any other amounts, one of the reactants will nearly always be entirely consumed, thus limiting the amount of product that may be generated. This substance is the limiting reactant, and the other substance is the excess reactant. Identifying the limiting and excess reactants for a given situation requires computing the molar amounts of each reactant provided and comparing them to the stoichiometric amounts represented in the balanced chemical equation. For example, imagine combining 3 moles of H₂ and 2 moles of Cl₂. This represents a 3:2 (or 1.5:1) ratio of hydrogen to chlorine present for reaction, which is greater than the stoichiometric ratio of 1:1. Hydrogen, therefore, is present in excess, and chlorine is the limiting reactant.

Reaction of all the provided chlorine (2 mol) will consume 2 mol of the 3 mol of hydrogen provided, leaving 1 mol of hydrogen unreacted.

An alternative approach to identifying the limiting reactant involves comparing the amount of product expected for the complete reaction of each reactant. Each reactant amount is used to separately calculate the amount of product that would be formed per the reaction’s stoichiometry. The reactant yielding the lesser amount of product is the limiting reactant

Mole Fraction and Molality

Several units commonly used to express the concentrations of solution components have been seen ,  each providing certain benefits for use in different applications. For example, molarity (M) is a convenient unit for use in stoichiometric calculations, since it is defined in terms of the molar amounts of solute species

 [ M = ( mol Solute / L solution) ]

Because solution volumes vary with temperature, molar concentrations will likewise vary. When expressed as molarity, the concentration of a solution with identical numbers of solute and solvent species will be different at different temperatures, due to the contraction/expansion of the solution. More appropriate for calculations involving many colligative properties are mole-based concentration units whose values are not dependent on temperature. Two such units are mole fraction  and molality.

The mole fraction, X, of a component is the ratio of its molar amount to the total number of moles of all solution components . By this definition, the sum of mole fractions for all solution components (the solvent and all solutes) is equal to one.

Molality is a concentration unit defined as the ratio of the numbers of moles of solute to the mass of the solvent in kilograms

ie [ m = mol Solute / Kg Solvent]

Since these units are computed using only masses and molar amounts, they do not vary with temperature and, thus, are better suited for applications requiring temperature-independent concentrations, including several colligative properties

Take Quiz

Access for free at openstax.org