Chemistry: The Central Science

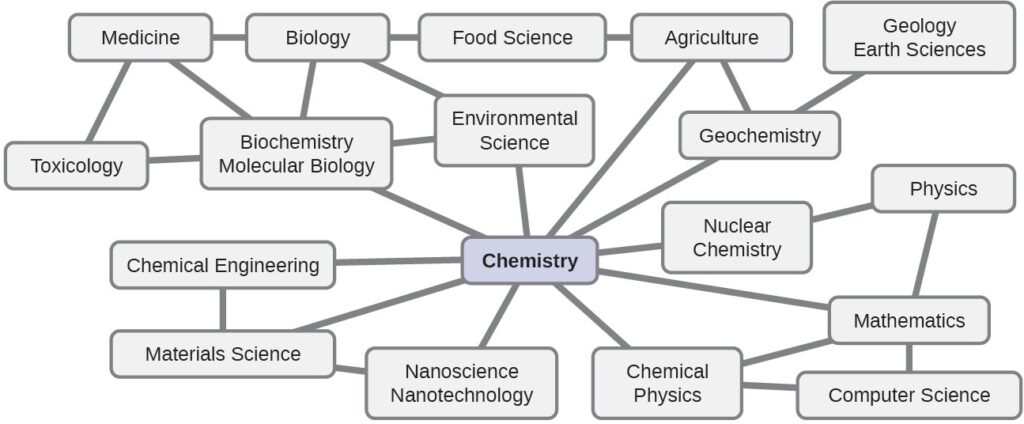
Chemistry is sometimes referred to as “the central science” due to its interconnectedness with a vast array of other STEM disciplines (STEM stands for areas of study in the science, technology, engineering, and math fields). Chemistry and the language of chemists play vital roles in biology, medicine, materials science, forensics, environmental science, and many other fields . The basic principles of physics are essential for understanding many aspects of chemistry, and there is extensive overlap between many subdisciplines within the two fields, such as chemical physics and nuclear chemistry. Mathematics, computer science, and information theory provide important tools that help us calculate, interpret, describe, and generally make sense of the chemical world. Biology and chemistry converge in biochemistry, which is crucial in  understanding the many complex factors and processes that keep living organisms (such as us) alive. Chemical engineering, materials science, and nanotechnology combine chemical principles and empirical findings to produce useful substances, ranging from gasoline to fabrics to electronics. Agriculture, food science, veterinary science, and brewing and wine making help provide sustenance in the form of food and drink to the world’s population. Medicine, pharmacology, biotechnology, and botany identify and produce substances that help keep us healthy. Environmental science, geology, oceanography, and atmospheric science incorporate many chemical ideas to help us better understand and protect our physical world. Chemical ideas are used to help understand the universe in astronomy and cosmology.

The Scientific Method

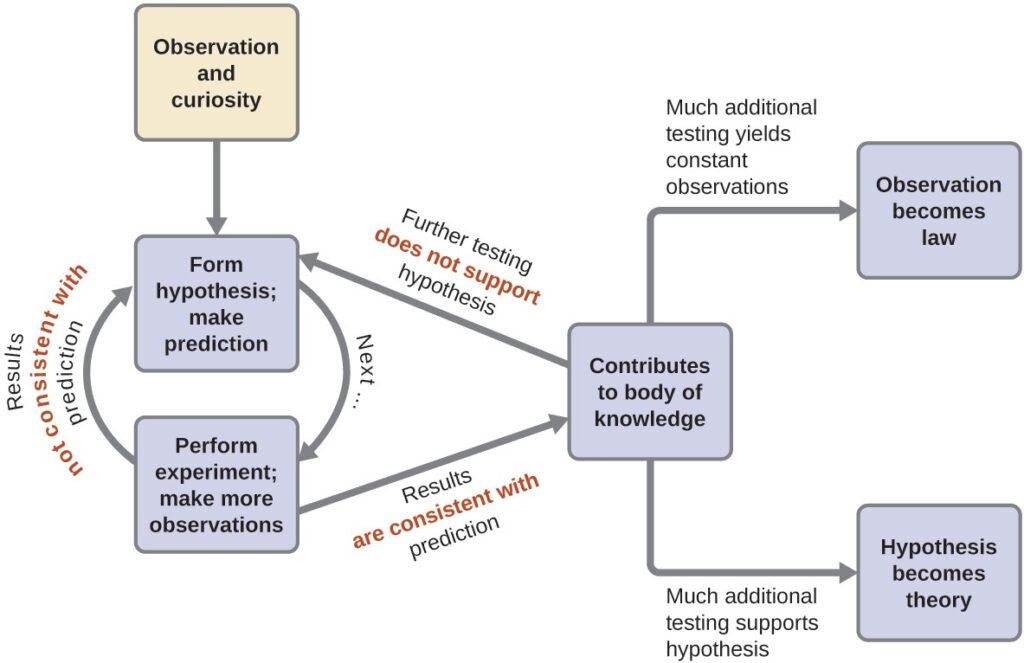
Chemistry is a science based on observation and experimentation. Doing chemistry involves attempting to answer questions and explain observations in terms of the laws and theories of chemistry, using procedures that are accepted by the scientific community. There is no single route to answering a question or explaining an observation, but there is an aspect common to every approach: Each uses knowledge based on experiments that can be reproduced to verify the results. Some routes involve a hypothesis, a tentative explanation of

observations that acts as a guide for gathering and checking information. A hypothesis is tested by experimentation, calculation, and/or comparison with the experiments of others and then refined as needed.

Some hypotheses are attempts to explain the behavior that is summarized in laws. The laws of science summarize a vast number of experimental observations, and describe or predict some facet of the natural world. If such a hypothesis turns out to be capable of explaining a large body of experimental data, it can reach the status of a theory. Scientific theories are well-substantiated, comprehensive, testable explanations of particular aspects of nature. Theories are accepted because they provide satisfactory explanations, but they can be modified if new data become available. The path of discovery that leads from question and observation to law or hypothesis to theory, combined with experimental verification of the hypothesis and any necessary modification of the theory, is called the scientific method

Phases and Classification of Matter

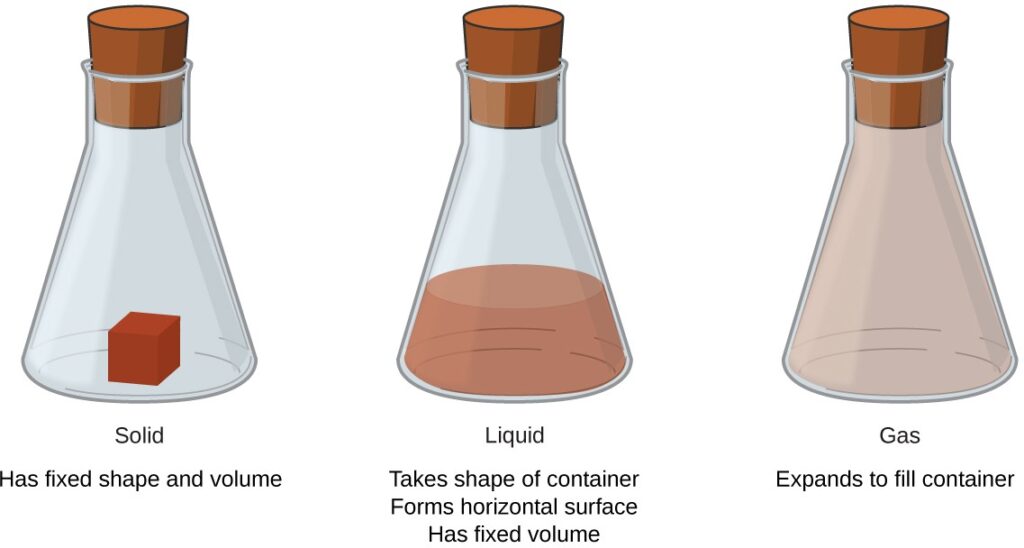
Matter is defined as anything that occupies space and has mass, and it is all around us. Solids and liquids are more obviously matter: We can see that they take up space, and their weight tells us that they have mass. Gases are also matter; if gases did not take up space, a balloon would not inflate (increase its volume) when filled with gas. Solids, liquids, and gases are the three states of matter commonly found on earth .

A solid is rigid and possesses a definite shape. A liquid flows and takes the shape of its container, except that it forms a flat or slightly curved upper surface when acted upon by gravity. (In zero gravity, liquids assume a spherical shape.) Both liquid and solid samples have volumes that are very nearly independent of pressure. A gas takes both the shape and volume of its container.

A fourth state of matter, plasma, occurs naturally in the interiors of stars. A plasma is a gaseous state of matter that contains appreciable numbers of electrically charged particles . The presence of these charged particles imparts unique properties to plasmas that justify their classification as a state of matter distinct from gases. In addition to stars, plasmas are found in some other high-temperature environments (both natural and man-made), such as lightning strikes, certain television screens, and specialized analytical instruments used to detect trace amounts of metals

Some samples of matter appear to have properties of solids, liquids, and/or gases at the same time. This can occur when the sample is composed of many small pieces. For example, we can pour sand as if it were a liquid because it is composed of many small grains of solid sand. Matter can also have properties of more than one state when it is a mixture, such as with clouds. Clouds appear to behave somewhat like gases, but they are actually mixtures of air (gas) and tiny particles of water (liquid or solid).

The mass of an object is a measure of the amount of matter in it. One way to measure an object’s mass is to measure the force it takes to accelerate the object. It takes much more force to accelerate a car than a bicycle because the car has much more mass. A more common way to determine the mass of an object is to use a balance to compare its mass with a standard mass.

Although weight is related to mass, it is not the same thing. Weight refers to the force that gravity exerts on an object. This force is directly proportional to the mass of the object. The weight of an object changes as the force of gravity changes, but its mass does not. An astronaut’s mass does not change just because she goes to the moon. But her weight on the moon is only one-sixth her earth-bound weight because the moon’s gravity is only one-sixth that of the earth’s. She may feel “weightless” during her trip when she experiences negligible external forces (gravitational or any other), although she is, of course, never “massless.”

The law of conservation of matter summarizes many scientific observations about matter: It states that there is no detectable change in the total quantity of matter present when matter converts from one type to another (a chemical change) or changes among solid, liquid, or gaseous states (a physical change).

Classifying Matter

Matter can be classified into several categories. Two broad categories are mixtures and pure substances. A pure substance has a constant composition. All specimens of a pure substance have exactly the same makeup and properties. Any sample of sucrose (table sugar) consists of 42.1% carbon, 6.5% hydrogen, and 51.4% oxygen by mass. Any sample of sucrose also has the same physical properties, such as melting point, color, and sweetness, regardless of the source from which it is isolated.

Pure substances may be divided into two classes: elements and compounds. Pure substances that cannot be broken down into simpler substances by chemical changes are called elements. Iron, silver, gold, aluminum, sulfur, oxygen, and copper are familiar examples of the more than 100 known elements, of which about 90 occur naturally on the earth, and two dozen or so have been created in laboratories.

Pure substances that are comprised of two or more elements are called compounds. Compounds may be broken down by chemical changes to yield either elements or other compounds, or both. Mercury(II) oxide, an orange, crystalline solid, can be broken down by heat into the elements mercury and oxygen .

When heated in the absence of air, the compound sucrose is broken down into the element carbon and the compound water. (The initial stage of this process, when the sugar is turning brown, is known as caramelization—this is what imparts the characteristic sweet and nutty flavor to caramel apples, caramelized onions, and caramel). Silver(I) chloride is a white solid that can be broken down into its elements, silver and chlorine, by absorption of light. This property is the basis for the use of this compound in photographic films and photochromic eyeglasses (those with lenses that darken when exposed to light

The properties of combined elements are different from those in the free, or uncombined, state. For example, white crystalline sugar (sucrose) is a compound resulting from the chemical combination of the element carbon, which is a black solid in one of its uncombined forms, and the two elements hydrogen and oxygen, which are colorless gases when uncombined. Free sodium, an element that is a soft, shiny, metallic solid, and free chlorine, an element that is a yellow-green gas, combine to form sodium chloride (table salt), a compound that is a white, crystalline solid.

A mixture is composed of two or more types of matter that can be present in varying amounts and can be separated by physical changes, such as evaporation (you will learn more about this later). A mixture with a composition that varies from point to point is called a heterogeneous mixture. Some examples of heterogeneous mixtures are chocolate chip cookies (we can see the separate bits of chocolate, nuts, and cookie dough) and granite (we can see the quartz, mica, feldspar, and more).

Although there are just over 100 elements, tens of millions of chemical compounds result from different combinations of these elements. Each compound has a specific composition and possesses definite chemical and physical properties that distinguish it from all other compounds. And, of course, there are innumerable ways to combine elements and compounds to form different mixtures. A summary of how to distinguish between the various major classifications of matter is shown in the below figure

Eleven elements make up about 99% of the earth’s crust and atmosphere . Oxygen constitutes nearly one-half and silicon about one-quarter of the total quantity of these elements. A majority of elements on earth are found in chemical combinations with other elements; about one-quarter of the elements are also found in the free state

Elemental Composition of Earth

Element	Symbol	Percent Mass	Element	Symbol	Percent Mass
oxygen	O	49.20	chlorine	Cl	0.19
silicon	Si	25.67	phosphorus	P	0.11
aluminum	Al	7.50	manganese	Mn	0.09
iron	Fe	4.71	carbon	C	0.08
calcium	Ca	3.39	sulfur	S	0.06
sodium	Na	2.63	barium	Ba	0.04
potassium	K	2.40	nitrogen	N	0.03
magnesium	Mg	1.93	fluorine	F	0.03
hydrogen	H	0.87	strontium	Sr	0.02
titanium	Ti	0.58	all others	–	0.47

Atoms and Molecules

An atom is the smallest particle of an element that has the properties of that element and can enter into a chemical combination. Consider the element gold, for example. Imagine cutting a gold nugget in half, then cutting one of the halves in half, and repeating this process until a piece of gold remained that was so small that it could not be cut in half (regardless of how tiny your knife may be). This minimally sized piece of gold is an atom (from the Greek atomos, meaning “indivisible”). This atom would no longer be gold if it were divided any further

An atom is so small that its size is difficult to imagine. One of the smallest things we can see with our unaided eye is a single thread of a spider web: These strands are about 1/10,000 of a centimeter (0.0001 cm) in diameter. Although the cross-section of one strand is almost impossible to see without a microscope, it is huge on an atomic scale

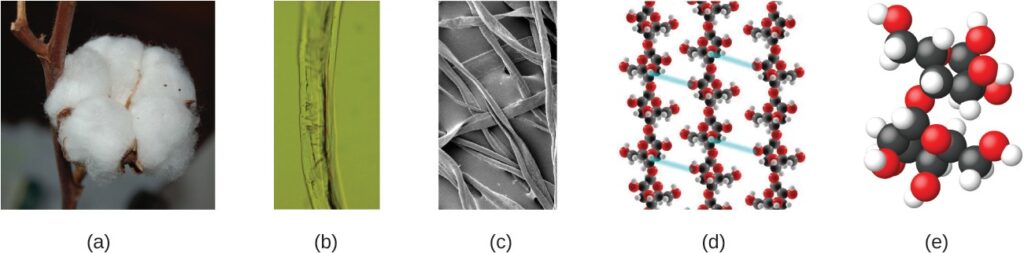
The above images provide an increasingly closer view: (a) a cotton boll, (b) a single cotton fiber viewed under an optical microscope (magnified 40 times), (c) an image of a cotton fiber obtained with an electron microscope (much higher magnification than with the optical microscope); and (d and e) atomic-level models of the fiber (spheres of different colors represent atoms of different elements). (credit c: modification of work by “Featheredtar”/Wikimedia Commons)

An atom is so light that its mass is also difficult to imagine. A billion lead atoms (1,000,000,000 atoms) weigh about 3 X 10−13 grams, a mass that is far too light to be weighed on even the world’s most sensitive balances. It would require over 300,000,000,000,000 lead atoms (300 trillion, or 3      1014) to be weighed, and they would weigh only 0.0000001 gram

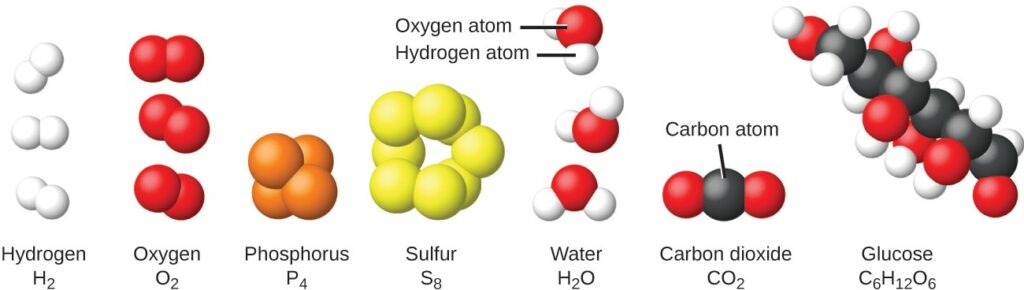
It is rare to find collections of individual atoms. Only a few elements, such as the gases helium, neon, and argon, consist of a collection of individual atoms that move about independently of one another. Other elements, such as the gases hydrogen, nitrogen, oxygen, and chlorine, are composed of units that consist of pairs of atoms . One form of the element phosphorus consists of units composed of four phosphorus atoms. The element sulfur exists in various forms, one of which consists of units composed of eight sulfur atoms. These units are called molecules. A molecule consists of two or more atoms joined by strong forces called chemical bonds. The atoms in a molecule move around as a unit, much like the cans of soda in a six-pack or a bunch of keys joined together on a single key ring. A molecule may consist of two or more identical atoms, as in the molecules found in the elements hydrogen, oxygen, and sulfur, or it may consist of two or more different atoms, as in the molecules found in water. Each water molecule is a unit that contains two hydrogen atoms and one oxygen atom. Each glucose molecule is a unit that contains 6 carbon atoms, 12 hydrogen atoms, and 6 oxygen atoms. Like atoms, molecules are incredibly small and light.

Physical and Chemical Properties

The characteristics that distinguish one substance from another are called properties. A physical property is a characteristic of matter that is not associated with a change in its chemical composition. Familiar examples of physical properties include density, color, hardness, melting and boiling points, and electrical conductivity.

Some physical properties, such as density and color, may be observed without changing the physical state of the matter. Other physical properties, such as the melting temperature of iron or the freezing temperature of water, can only be observed as matter undergoes a physical change. A physical change is a change in the state or properties of matter without any accompanying change in the chemical identities of the substances contained in the matter. Physical changes are observed when wax melts, when sugar dissolves in coffee, and when steam condenses into liquid water . Other examples of physical changes include magnetizing and demagnetizing metals (as is done with common antitheft security tags) and grinding solids into powders (which can sometimes yield noticeable changes in color). In each of these examples, there is a change in the physical state, form, or properties of the substance, but no change in its chemical composition

(a) Wax undergoes a physical change when solid wax is heated and forms liquid wax. (b) Steam condensing inside a cooking pot is a physical change, as water vapor is changed into liquid water. (credit a: modification of work by “95jb14”/Wikimedia Commons; credit b: modification of work by “mjneuby”/Flickr)

The change of one type of matter into another type (or the inability to change) is a chemical property. Examples of chemical properties include flammability, toxicity, acidity, and many other types of reactivity. Iron, for example, combines with oxygen in the presence of water to form rust; chromium does not oxidize . Nitroglycerin is very dangerous because it explodes easily; neon poses almost no hazard because it is very unreactive

(a) One of the chemical properties of iron is that it rusts; (b) one of the chemical properties of chromium is that it does not. (credit a: modification of work by Tony Hisgett; credit b: modification of work by “Atoma”/Wikimedia Commons)

A chemical change always produces one or more types of matter that differ from the matter present before the change. The formation of rust is a chemical change because rust is a different kind of matter than the iron, oxygen, and water present before the rust formed. The explosion of nitroglycerin is a chemical change because the gases produced are very different kinds of matter from the original substance. Other examples of chemical changes include reactions that are performed in a lab (such as copper reacting with nitric acid), all forms of combustion (burning), and food being cooked, digested, or rotting

While many elements differ dramatically in their chemical and physical properties, some elements have similar properties. For example, many elements conduct heat and electricity well, whereas others are poor conductors. These properties can be used to sort the elements into three classes: metals (elements that conduct well), nonmetals (elements that conduct poorly), and metalloids (elements that have intermediate conductivities).

The periodic table is a table of elements that places elements with similar properties close together . You will learn more about the periodic table as you continue your study of chemistry

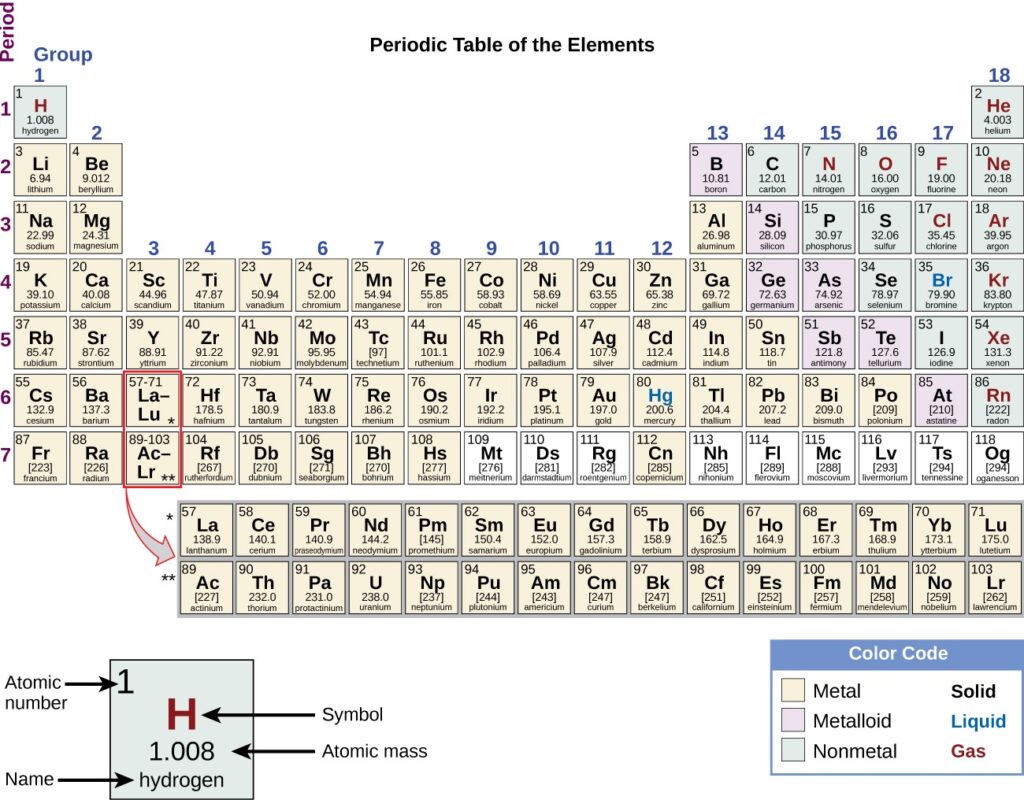
The periodic table shows how elements may be grouped according to certain similar properties. Note the background color denotes whether an element is a metal, metalloid, or nonmetal, whereas the element symbol color indicates whether it is a solid, liquid, or gas.

Measurements

Measurements provide much of the information that informs the hypotheses, theories, and laws describing the behavior of matter and energy in both the macroscopic and microscopic domains of chemistry. Every measurement provides three kinds of information:

1. the size or magnitude of the measurement (a number);
2. a standard of comparison for the measurement (a unit); and
3.  an indication of the uncertainty of the measurement.

While the number and unit are explicitly represented when a quantity is written, the uncertainty is an aspect of the measurement result that is more implicitly represented and will be discussed later.

The number in the measurement can be represented in different ways, including decimal form and scientific notation. (Scientific notation is also known as exponential notation). For example, the maximum takeoff weight of a Boeing 777-200ER airliner is 298,000 kilograms, which can also be written as 2.98 X 105 kg. The mass of the average mosquito is about 0.0000025 kilograms ,  which can be written as  2.5 X 10^-6  Kg  .

Units, such as liters, pounds, and centimeters, are standards of comparison for measurements. A 2-liter   

 bottle of a soft drink contains a volume of beverage that is twice that of the accepted volume of 1 liter.  Without units, a number can be meaningless, confusing, or possibly life threatening. Suppose a doctor prescribes phenobarbital to control a patient’s seizures and states a dosage of “100” without specifying units. Not only will this be confusing to the medical professional giving the dose, but the consequences can be dire.

The measurement units for seven fundamental properties (“base units”) are listed in the below table . The standards for these units are fixed by international agreement, and they are called the International System of Units or SI Units (from the French, Le Système International d’Unités). SI units have been used by the United States National Institute of Standards and Technology (NIST) since 1964. Units for other properties may be derived from these seven base units.

Base Units of the SI System

length	meter	m
mass	kilogram	kg
time	second	s
temperature	kelvin	K
electric current	ampere	A
amount of substance	mole	mol
luminous intensity	candela	cd

Everyday measurement units are often defined as fractions or multiples of other units . Fractional or multiple  SI units are named using a prefix and the name of the base unit. For example, a length of 1000 meters is also called a kilometer because the prefix kilo means “one thousand,” which in scientific notation is 103 (1 kilometer = 1000 m = 103 m). The prefixes used and the powers to which 10 are raised are listed in  the below table

Common Unit Prefixes                                               

femto	f	10−15	1 femtosecond (fs) = 1       10−15 s (0.000000000000001 s)
pico	p	10−12	1 picometer (pm) = 1       10−12 m (0.000000000001 m)

nano	n	10−9	4 nanograms (ng) = 4    10−9 g (0.000000004 g)
micro	µ	10−6	1 microliter (μL) = 1        10−6 L (0.000001 L)
milli	m	10−3	2 millimoles (mmol) = 2      10−3 mol (0.002 mol)
centi	c	10−2	7 centimeters (cm) = 7     10−2 m (0.07 m)
deci	d	10−1	1 deciliter (dL) = 1     10−1 L (0.1 L )
kilo	k	103	1 kilometer (km) = 1       103 m (1000 m)
mega	M	106	3 megahertz (MHz) = 3     106 Hz (3,000,000 Hz)
giga	G	109	8 gigayears (Gyr) = 8     109 yr (8,000,000,000 yr)
tera	T	1012	5 terawatts (TW) = 5      1012 W (5,000,000,000,000 W)

SI Base Units

The initial units of the metric system, which eventually evolved into the SI system, were established in France during the French Revolution. The original standards for the meter and the kilogram were adopted there in 1799 and eventually by other countries. This section introduces four of the SI base units commonly used in chemistry. Other SI units will be introduced in subsequent chapters.

Length

The standard unit of length in both the SI and original metric systems is the meter (m). A meter was originally specified as 1/10,000,000 of the distance from the North Pole to the equator. It is now defined as the distance light in a vacuum travels in 1/299,792,458 of a second. A meter is about 3 inches longer than a yard  , one meter is about 39.37 inches or 1.094 yards. Longer distances are often reported in kilometers (1 km

= 1000 m = 103 m), whereas shorter distances can be reported in centimeters (1 cm = 0.01 m = 10−2 m) or

millimeters (1 mm = 0.001 m = 10−3 m).

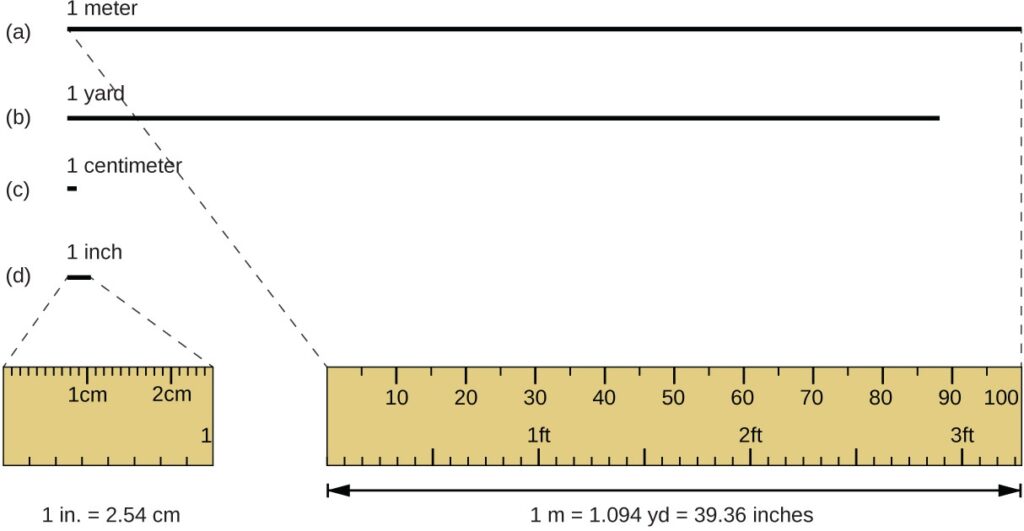
Above figure gives The relative lengths of 1 m, 1 yd, 1 cm, and 1 in. are shown (not actual size), as well as comparisons of 2.54 cm and  1 in., and of 1 m and 1.094 yd

Mass

The standard unit of mass in the SI system is the kilogram (kg). The kilogram was previously defined by the International Union of Pure and Applied Chemistry (IUPAC) as the mass of a specific reference object. This object was originally one liter of pure water, and more recently it was a metal cylinder made from a platinum- iridium alloy with a height and diameter of 39 mm as shown in below figure . In May 2019, this definition was changed to one that is based instead on precisely measured values of several fundamental physical constants. One kilogram is about 2.2 pounds. The gram (g) is exactly equal to 1/1000 of the mass of the kilogram (10−3 kg)

Temperature

Temperature is an intensive property. The SI unit of temperature is the kelvin (K). The IUPAC convention is to use kelvin (all lowercase) for the word, K (uppercase) for the unit symbol, and neither the word “degree” nor the degree symbol (°). The degree Celsius (°C) is also allowed in the SI system, with both the word “degree” and the degree symbol used for Celsius measurements. Celsius degrees are the same magnitude as those of kelvin, but the two scales place their zeros in different places. Water freezes at 273.15 K (0 °C) and boils at 373.15 K (100 °C) by definition, and normal human body temperature is approximately 310 K (37 °C).

Time

The SI base unit of time is the second (s). Small and large time intervals can be expressed with the appropriate prefixes; for example, 3 microseconds = 0.000003 s = 3×10⁻⁶ and 5 megaseconds = 5,000,000 s = 5  10⁶ s. Alternatively, hours, days, and years can be used.

Derived SI Units

We can derive many units from the seven SI base units. For example, we can use the base unit of length to define a unit of volume, and the base units of mass and length to define a unit of density.

Volume

Volume is the measure of the amount of space occupied by an object. The standard SI unit of volume is defined by the base unit of length . The standard volume is a cubic meter (m3), a cube with an edge length of exactly one meter. To dispense a cubic meter of water, we could build a cubic box with edge lengths of exactly one meter. This box would hold a cubic meter of water or any other substance.

A more commonly used unit of volume is derived from the decimeter (0.1 m, or 10 cm). A cube with edge lengths of exactly one decimeter contains a volume of one cubic decimeter (dm3). A liter (L) is the more common name for the cubic decimeter. One liter is about 1.06 quarts.

A cubic centimeter (cm3) is the volume of a cube with an edge length of exactly one centimeter. The abbreviation cc (for cubic centimeter) is often used by health professionals. A cubic centimeter is equivalent to a milliliter (mL) and is 1/1000 of a liter.

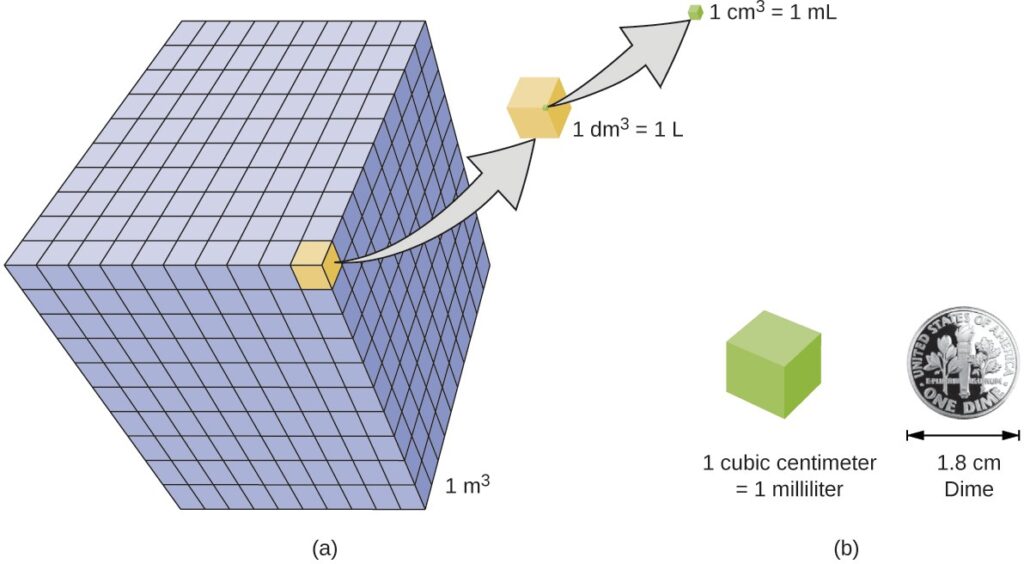
The relative volumes are shown for cubes of 1 m³, 1 dm³ (1 L), and 1 cm³ (1 mL) (not to scale). (b) The diameter of a dime is compared relative to the edge length of a 1-cm³ (1-mL) cube.

Density

We use the mass and volume of a substance to determine its density. Thus, the units of density are defined by the base units of mass and length. The density of a substance is the ratio of the mass of a sample of the substance to its volume. The SI unit for density is the kilogram per cubic meter (kg/m³). For many situations, however, this is an inconvenient unit, and we often use grams per cubic centimeter (g/cm³) for the densities of solids and liquids, and grams per liter (g/L) for gases. Although there are exceptions, most liquids and solids have densities that range from about 0.7 g/cm³ (the density of petrol ) to 19 g/cm³ (the density of gold). The density of air is about 1.2 g/L

Densities of Common Substances

Solids	Liquids	Gases (at 25 °C and 1 atm)
ice (at 0 °C) 0.92 g/cm3	water 1.0 g/cm3	dry air 1.20 g/L
oak (wood) 0.60–0.90 g/cm3	ethanol 0.79 g/cm3	oxygen 1.31 g/L
iron 7.9 g/cm3	acetone 0.79 g/cm3	nitrogen 1.14 g/L
copper 9.0 g/cm3	glycerin 1.26 g/cm3	carbon dioxide 1.80 g/L
lead 11.3 g/cm3	olive oil 0.92 g/cm3	helium 0.16 g/L
silver 10.5 g/cm3	gasoline 0.70–0.77 g/cm3	neon 0.83 g/L
gold 19.3 g/cm3	mercury 13.6 g/cm3	radon 9.1 g/L

While there are many ways to determine the density of an object, perhaps the most straightforward method involves separately finding the mass and volume of the object, and then dividing the mass of the sample by its volume. In the following example, the mass is found directly by weighing, but the volume is found indirectly through length measurements

Density = Mass / Volume

Measurement Uncertainty, Accuracy, and Precision

Counting is the only type of measurement that is free from uncertainty, provided the number of objects being counted does not change while the counting process is underway. The result of such a counting measurement is an example of an exact number. By counting the eggs in a carton, one can determine exactly how many eggs the carton contains. The numbers of defined quantities are also exact. By definition, 1 foot is exactly 12 inches, 1 inch is exactly 2.54 centimeters, and 1 gram is exactly 0.001 kilogram. Quantities derived from measurements other than counting, however, are uncertain to varying extents due to practical limitations of the measurement process used.

Significant Figures in Measurement

The numbers of measured quantities, unlike defined or directly counted quantities, are not exact. To measure the volume of liquid in a graduated cylinder (below figure) ,  you should make a reading at the bottom of the meniscus, the lowest point on the curved surface of the liquid

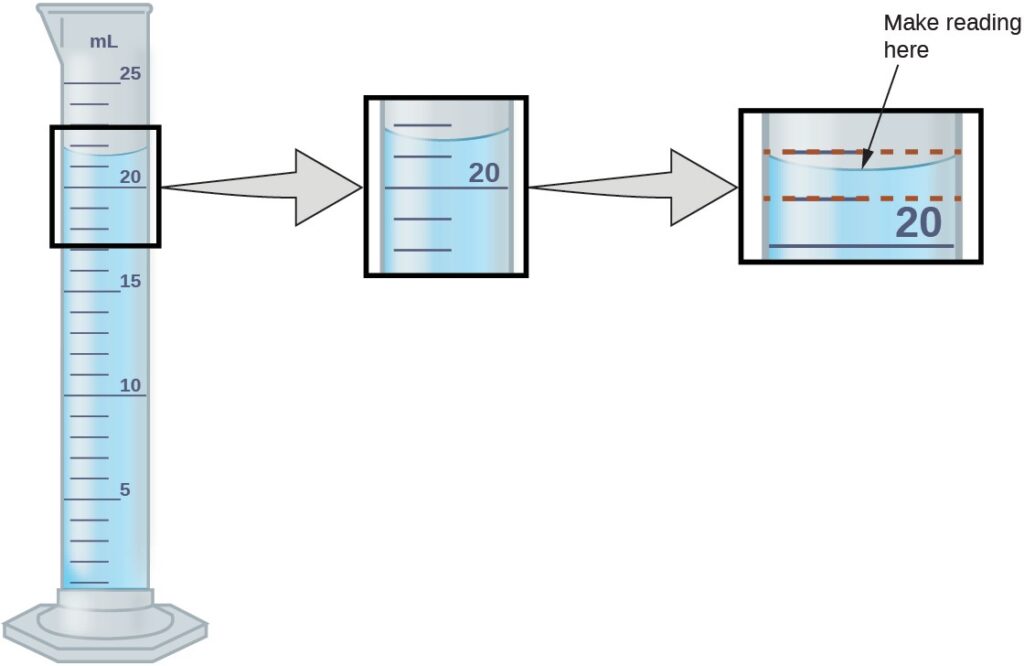
Refer to the above  illustration . The bottom of the meniscus in this case clearly lies between the 21 and 22 markings, meaning the liquid volume is certainly greater than 21 mL but less than 22 mL. The meniscus appears to be a bit closer to the 22-mL mark than to the 21-mL mark, and so a reasonable estimate of the liquid’s volume would be 21.6 mL. In the number 21.6, then, the digits 2 and 1 are certain, but the 6 is an estimate. Some people might estimate the meniscus position to be equally distant from each of the markings and estimate the tenth-place digit as 5, while others may think it to be even closer to the 22-mL mark and estimate this digit to be 7. Note that it would be pointless to attempt to estimate a digit for the hundredths place, given that the tenths-place digit is uncertain. In general, numerical scales such as the one on this graduated cylinder will permit measurements to one-tenth of the smallest scale division. The scale in this case has 1-mL divisions, and so volumes may be measured to the nearest 0.1 mL.

This concept holds true for all measurements, even if you do not actively make an estimate. If you place a quarter on a standard electronic balance, you may obtain a reading of 6.72 g. The digits 6 and 7 are certain, and the 2 indicates that the mass of the quarter is likely between 6.71 and 6.73 grams. The quarter weighs about 6.72 grams, with a nominal uncertainty in the measurement of ± 0.01 gram. If the coin is weighed on a more sensitive balance, the mass might be 6.723 g. This means its mass lies between 6.722 and 6.724 grams, an uncertainty of 0.001 gram. Every measurement has some uncertainty, which depends on the device used (and the user’s ability). All of the digits in a measurement, including the uncertain last digit, are called significant figures or significant digits. Note that zero may be a measured value; for example, if you stand on a scale that shows weight to the nearest Kg ,  and it shows “120,” then the 1 (hundreds), 2 (tens) and 0 (ones) are all significant (measured) values.

Significant Figures in Calculations

A second important principle of uncertainty is that results calculated from a measurement are at least as uncertain as the measurement itself. Take the uncertainty in measurements into account to avoid misrepresenting the uncertainty in calculated results. One way to do this is to report the result of a calculation with the correct number of significant figures, which is determined by the following three rules for rounding numbers:

1. When adding or subtracting numbers, round the result to the same number of decimal places as the         number with the least number of decimal places (the least certain value in terms of addition and subtraction).
2. When multiplying or dividing numbers, round the result to the same number of digits as the number with the least number of significant figures (the least certain value in terms of multiplication and division).
3. If the digit to be dropped (the one immediately to the right of the digit to be retained) is less than 5, “round down” and leave the retained digit unchanged; if it is more than 5, “round up” and increase the retained digit by 1. If the dropped digit is 5, and it’s either the last digit in the number or it’s followed only by zeros, round up or down, whichever yields an even value for the retained digit. If any nonzero digits follow the dropped 5, round up. (The last part of this rule may strike you as a bit odd, but it’s based on reliable statistics and is aimed at avoiding any bias when dropping the digit “5,” since it is equally close to both possible values of the retained digit.)

Conversion Factors and Dimensional Analysis

A ratio of two equivalent quantities expressed with different measurement units can be used as a unit conversion factor. For example, the lengths of 2.54 cm and 1 inch. are equivalent (by definition), and so a unit conversion factor may be derived from the ratio

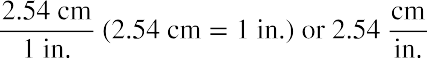
Common Conversion Factors

Length	Volume	Mass
1 m = 1.0936 yd	1 L = 1.0567 qt	1 kg = 2.2046 lb
1 in. = 2.54 cm (exact)	1 qt = 0.94635 L	1 lb = 453.59 g
1 km = 0.62137 mi	1 ft3 = 28.317 L	1 (avoirdupois) oz = 28.349 g
1 mi = 1609.3 m	1 tbsp = 14.787 mL	1 (troy) oz = 31.103 g

When a quantity (such as distance in inches) is multiplied by an appropriate unit conversion factor, the quantity is converted to an equivalent value with different units (such as distance in centimeters).

Take Quiz

Access for free at openstax.org